Shortest Paths

1. Reading
2. Introduction
3. Dijkstra's algorithm
4. Exercise
5. Practice Problems

1 Reading

2 Introduction

Done: BFS to find the minimum path length from v to u in \(O(|E|+|V|)\)
Actually, can find the minimum path length from v to every node
- Still \(O(|E|+|V|)\)
No faster way for a "distinguished" destination in the worst-case
Today: Weighted graphs
- Given a weighted graph and node v, find the minimum-cost path from v to every node
- As before, asymptotically no harder than for one destination
- Unlike before, BFS will not work
Why BFS won't work: Shortest path may not have the fewest edges
- Annoying when this happens with costs of flights
We will assume there are no negative weights
- Problem is ill-defined if there are negative-cost cycles
- Today's algorithm is wrong if edges can be negative
- There are other, slower (but not terrible) algorithms

3 Dijkstra's algorithm

Algorithm named after its inventor Edsger Dijkstra (1930-2002)
- A good quotation: "computer science is no more about computers than astronomy is about telescopes"
The idea: reminiscent of BFS, but adapted to handle weights
- Grow the set of nodes whose shortest distance has been computed
- Nodes not in the set will have a "best distance so far"
- A priority queue will turn out to be useful for efficiency
Initially, start node has cost 0 and all other nodes have cost \(\infty\)
At each step:
- Pick closest unknown vertex v
- Add it to the set of known vertices
- Update distances for nodes with edges from v

3.1 The Algorithm

For each node v, set v.cost = infinity and v.known = false
Set source.cost = 0
While there are unknown nodes in the graph
   Select the unknown node v with lowest cost
   Mark v as known
   For each edge (v,u) with weight w,
        c1 = v.cost + w    // cost of best path through v to u   
        c2 = u.cost        // cost of best path to u previously known
        if(c1 < c2){       // if the path through v is better
            u.cost = c1
            u.path = v     // for computing actual paths
        }

When a vertex is marked known, the cost of the shortest path to that node is known
- The path is also known by following back-pointers
While a vertex is still not known, another shorter path to it might still be found

3.2 Examples

See these slides

3.3 Greedy Algorithm

Dijkstra’s algorithm is an example of a greedy algorithm:
- At each step, always does what seems best at that step
  - A locally optimal step, not necessarily globally optimal
- Once a vertex is known, it is not revisited
  - Turns out to be globally optimal

3.4 Analyzing Efficiency

Had a problem: Compute shortest paths in a weighted graph with no negative weights
Learned an algorithm: Dijkstra's algorithm
What should we do after learning an algorithm?
- Analyze its efficiency
  - Will do better by using a data structure we learned earlier!

Pseudocode:

dijkstra(Graph G, Node start) {
  for each node: x.cost=infinity, x.known=false // initialization: O(|V|)
  start.cost = 0
  while(not all nodes are known) {
    b = find unknown node with smallest cost    // finding the smallest-cost node
    b.known = true                              // once for each node: O(|V|**2)
    for each edge (b,a) in G                    // processing edges: O(|E|)
      if(!a.known) {
        if(b.cost + weight((b,a)) < a.cost) {
          a.cost = b.cost + weight((b,a))
          a.path = b
        }
    }
}

So far: \(O(|V|^2)\)
We had a similar "problem" with topological sort being \(O(|V|^2)\) due to each iteration looking for the node to process next
- We solved it with a queue of zero-degree nodes
- But here we need the lowest-cost node and costs can change as we process edges

Solution?

A priority queue holding all unknown nodes, sorted by cost
But must support decreaseKey operation
- Must maintain a reference from each node to its current position in the priority queue
- Conceptually simple, but can be a pain to code up

dijkstra(Graph G, Node start) {
  for each node: x.cost=infinity, x.known=false // initialization: O(|V|)
  start.cost = 0
  build a heap with all nodes
  while(heap is not empty) {
    b = removeMin()                             // finding the smallest-cost node
    b.known = true                              // once for each node: O(|V|log|V|)
    for each edge (b,a) in G                    // processing edges: O(|E|log|V|)
      if(!a.known) {
        if(b.cost + weight((b,a)) < a.cost) {
          decreaseKey(a, b.cost + weight((b,a) - a.cost)
          a.path = b
        }
    }
}

Second approach: \(O(|V|\log |V| + |E|\log |V|)\)
- Better for sparse, but worse for dense

4 Exercise

Perhaps using this BFS implementation as a starting point, implement Dijkstra's algorithm. The Java PriorityQueue does not have a decreaseKey operation, so use IndexMinPQ from algs4. Here is a starter project you should use: ./dijkstras.zip. Here is documentation on relevant algs4 classes: EdgeWeightedGraph, DirectedEdge, IndexMinPQ.

Solution:

import java.util.LinkedList;

import edu.princeton.cs.algs4.DirectedEdge;
import edu.princeton.cs.algs4.EdgeWeightedDigraph;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.IndexMinPQ;
import edu.princeton.cs.algs4.StdOut;

public class Dijkstras {
    private double[] distTo; // distTo[v] = distance of shortest s->v path
    private DirectedEdge[] edgeTo; // edgeTo[v] = last edge on shortest s->v path
    private IndexMinPQ<Double> pq; // priority queue of vertices

    public Dijkstras(EdgeWeightedDigraph G, int s) {
        // initialize data structures
        distTo = new double[G.V()];
        edgeTo = new DirectedEdge[G.V()];
        boolean[] known = new boolean[G.V()];
        pq = new IndexMinPQ<>(G.V());

        // initialize distances
        for (int v = 0; v < known.length; v++) {
            if (v != s) {
                distTo[v] = Double.POSITIVE_INFINITY;
            }
            pq.insert(v, distTo[v]);
        }

        // run algorithm
        while (!pq.isEmpty()) {
            int v = pq.delMin();
            known[v] = true;
            for (DirectedEdge e : G.adj(v)) {
                if (!known[e.to()] && distTo[v] + e.weight() < distTo[e.to()]) {
                    distTo[e.to()] = distTo[v] + e.weight();
                    edgeTo[e.to()] = e;
                    pq.decreaseKey(e.to(), distTo[e.to()]);
                }
            }
        }
    }

    /**
     * Returns the length of a shortest path from the source vertex s to
     * vertex v.
     */
    public double distTo(int v) {
        return distTo[v];
    }

    /**
     * Returns true if there is a path from the source vertex s to vertex v.
     */
    public boolean hasPathTo(int v) {
        return distTo[v] < Double.POSITIVE_INFINITY;
    }

    /**
     * Returns a shortest path from the source vertex s to vertex v.
     */
    public Iterable<DirectedEdge> pathTo(int v) {
        if (!hasPathTo(v))
            return null;
        LinkedList<DirectedEdge> path = new LinkedList<>();
        DirectedEdge e = edgeTo[v];
        while (e != null) {
            path.addFirst(e);
            e = edgeTo[e.from()];
        }
        return path;
    }

    public static void main(String[] args) {
        In in = new In("tinyEWD.txt");
        EdgeWeightedDigraph G = new EdgeWeightedDigraph(in);
        int s = 0;

        // compute shortest paths
        Dijkstras sp = new Dijkstras(G, s);

        // print shortest path
        for (int t = 0; t < G.V(); t++) {
            if (sp.hasPathTo(t)) {
                StdOut.printf("%d to %d (%.2f)  ", s, t, sp.distTo(t));
                for (DirectedEdge e : sp.pathTo(t)) {
                    StdOut.print(e + "   ");
                }
                StdOut.println();
            } else {
                StdOut.printf("%d to %d         no path\n", s, t);
            }
        }
    }

    /**
     * Expected output:
     * 0 to 0 (0.00)  
     * 0 to 1 (1.05)  0->4  0.38   4->5  0.35   5->1  0.32   
     * 0 to 2 (0.26)  0->2  0.26   
     * 0 to 3 (0.99)  0->2  0.26   2->7  0.34   7->3  0.39   
     * 0 to 4 (0.38)  0->4  0.38   
     * 0 to 5 (0.73)  0->4  0.38   4->5  0.35   
     * 0 to 6 (1.51)  0->2  0.26   2->7  0.34   7->3  0.39   3->6  0.52   
     * 0 to 7 (0.60)  0->2  0.26   2->7  0.34
     */
}

5 Practice Problems¹

Explain why it is sometimes more efficient to compute the distance from a single source to all other nodes, even though a particular query may be answered with a partial solution.
Step through Dijkstra's algorithm to calculate the single-source shortest paths from A to every other vertex. Show your steps in the table below. Cross out old values and write in new ones, from left to right within each cell, as the algorithm proceeds. Also list the vertices in the order which you marked them known. Finally, indicate the lowest-cast path from node A to node G.
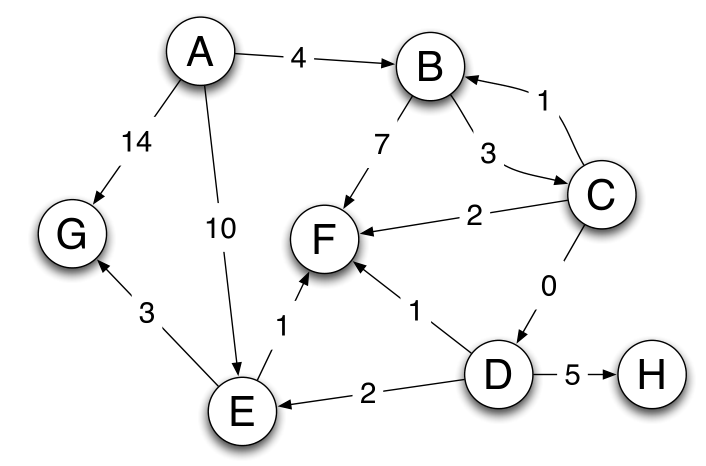
Given the graph above, list one possible order that vertices in the graph above would be processed if a breadth first traversal is done starting at A.
True or false. Adding a constant to every edge weight does not change the solution to the single-source shortest-paths problem.

Footnotes:

Solutions:

This can happen if multiple queries are made regarding a single source. One calculation of all solutions is less expensive than computing several partial solutions; some aspects of different solutions are shared.
Completed table:
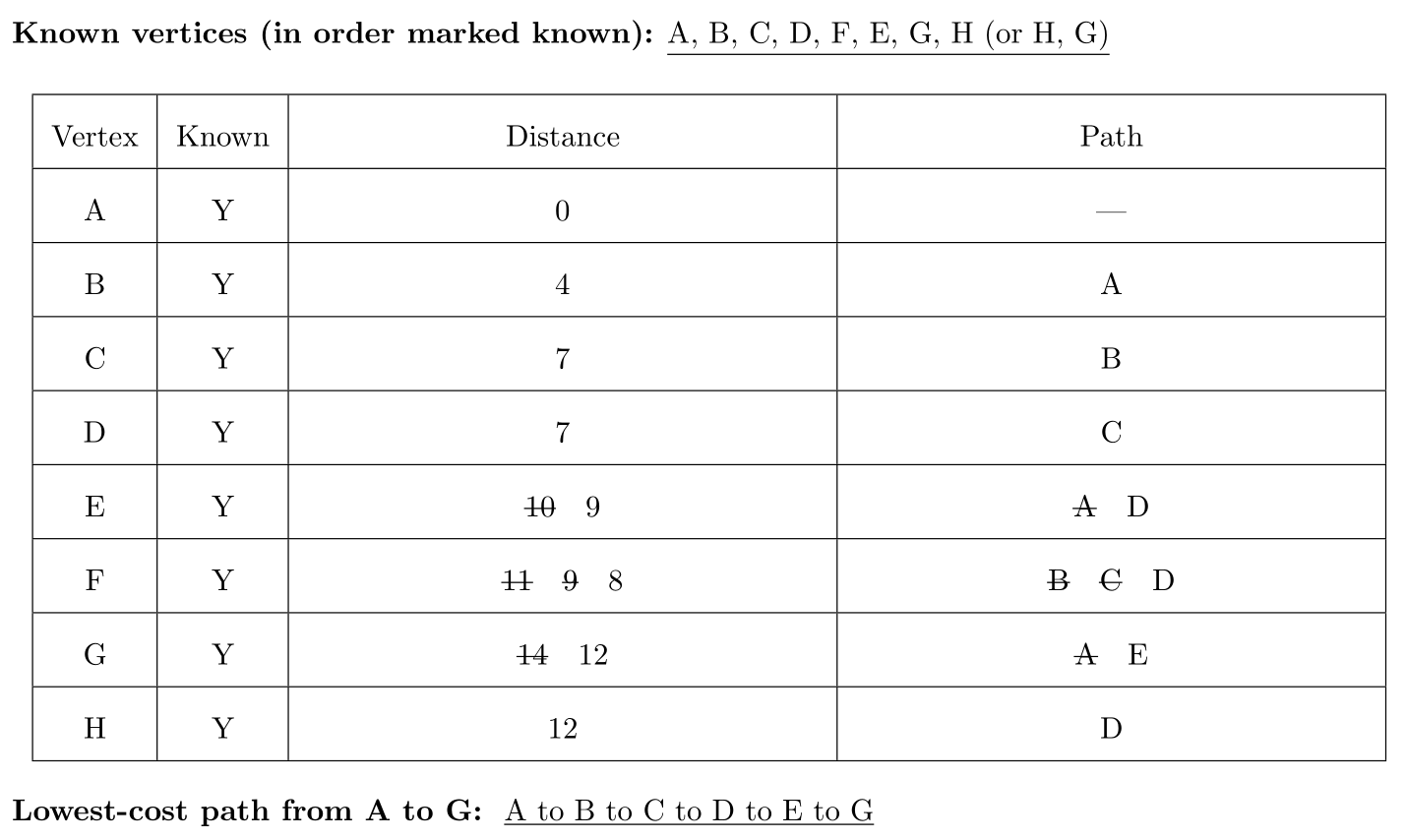
For a given distance, the vertices can be in any order.

Distance away 0 1 2 3 4

A B E G F C D H
False. The number of edges in a shortest path will affect the amount its cost increases from adding a constant to all edge weights.

Shortest Paths

Table of Contents

1 Reading

2 Introduction

3 Dijkstra's algorithm

3.1 The Algorithm

3.2 Examples

3.3 Greedy Algorithm

3.4 Analyzing Efficiency

4 Exercise

5 Practice Problems1

Footnotes:

5 Practice Problems¹