Priority Queues and Heaps
Table of Contents
1 Reading
Read Algorithms 2.4
2 Learning Goals
After this lesson you will be able to
- Describe the priority queue ADT and some of its applications
- Use the heap data structure to implement a priority queue
- Perform operations on a heap
3 Priority Queue ADT
A priority queue is a queue-like data structure that stores elements with data and comparable priorities. You might say that the largest priority value is the most important, or that the smallest is the most important (e.g., is "priority 100" or "priority 1" the most important). This is simply a convention and the ADT functions similarly either way. For this lesson I will treat the smallest priority as the most important: "priority 1" is more important than "priority 4".
The priority queue ADT defines three primary operations:
add: add an element to the queuegetMin: return the most important elementremoveMin: remove and return the most important elementisEmpty: are there elements left in the queue?
3.1 Applications
- Like all good ADTs, the priority queue arises often
- Sometimes blatant, sometimes less obvious
- It is useful when an operating system is running multiple programs
- "critical" before "interactive" before "compute-intensive"
- Maybe let users set priority level
- Treat hospital patients in order of severity (or triage)
- Select print jobs in order of decreasing length?
- Forward network packets in order of urgency
- Select most frequent symbols for data compression (technique called Huffman Coding)
- Sorting (first insert all, then repeatedly deleteMin)
- Greedy algorithms can make use of a priority queue
- We will see an example when we study graphs
- Discrete event simulation (system simulation, virtual worlds, …)
- Each event e happens at some time t, updating system state and generating new events \(e_1, \dots, e_n\) at times \(t+t_1, \dots, t+t_n\)
- Naive approach: advance "clock": by 1 unit at a time and process any events that happen then
- Better:
- Pending events in a priority queue (priority = event time)
- Repeatedly:
removeMinand thenaddnew events - Effectively set clock ahead to next event
3.2 Choice of Data Structure
| Operation | Unsorted array | Sorted circular array | Balanced BST (e.g., AVL Tree) |
|---|---|---|---|
add |
add at end: \(O(1)\) | add at right place/shift: \(O(n)\) | add at right place: \(O(\log n)\) |
removeMin |
search/shift: \(O(n)\) | move "front" of array: \(O(1)\) | leftmost node: \(O(\log n)\) |
In this lesson will will see a data structure called a binary heap.
- \(O(\log n)\)
addandremoveMin - Very good constant factors
- If elements added in a random order,
addis \(O(1)\) on average - Good performance is possible because the binary heap doesn't support unneeded operations—no need to maintain elements in full sorted order
4 Defining a Binary Heap
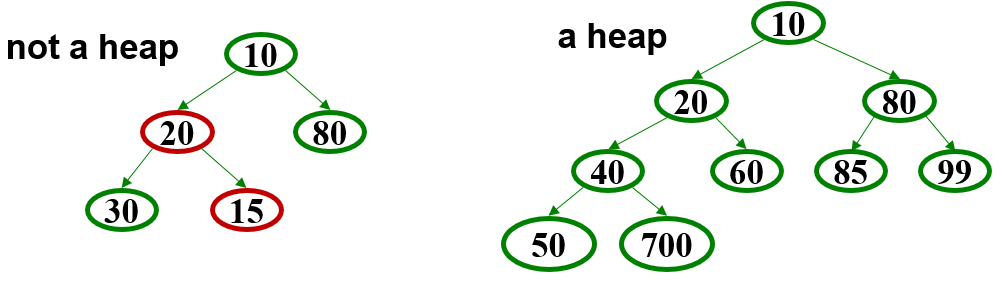
A binary min-heap (or just binary heap or just heap) is:
- Structure property: A complete binary tree
- We previously discussed how a full tree is one with all levels filled out—the maximum number of nodes for a given height
- A complete tree is one that that is full except for the lowest level, which must be partially filled in from left to right.
- Heap property: The priority of every node is more important than the priority of its descendents
- NOT a binary search tree
So:
- Where is the most important element? At the root
- What is the height of a heap with \(n\) elements? \(\log n\)
4.1 Operations
Overall strategy: preserve the structure property; break and restore heap property
getMin: returnroot.dataremoveMin:answer = root.data- Move right-most node in bottom row to the root to restore the structure property
- Percolate down to restore the heap property
add:- Put new node in the next open position on bottom row to restore structure property
- Percolate up to restore the heap property
4.1.1 removeMin
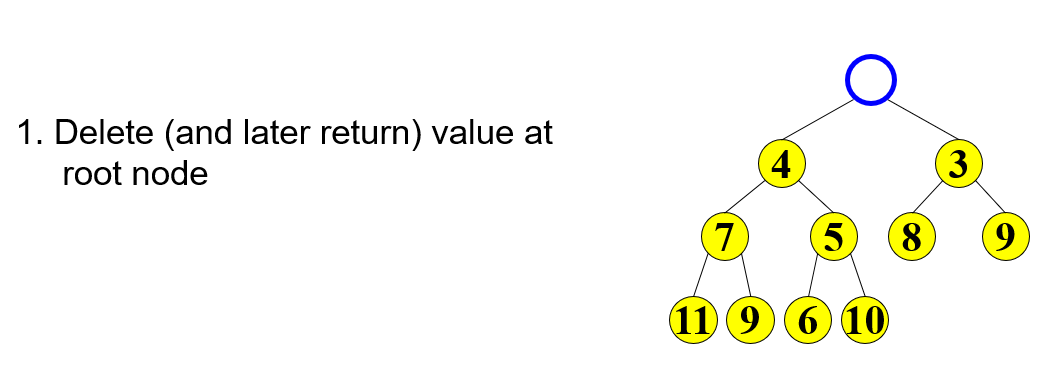
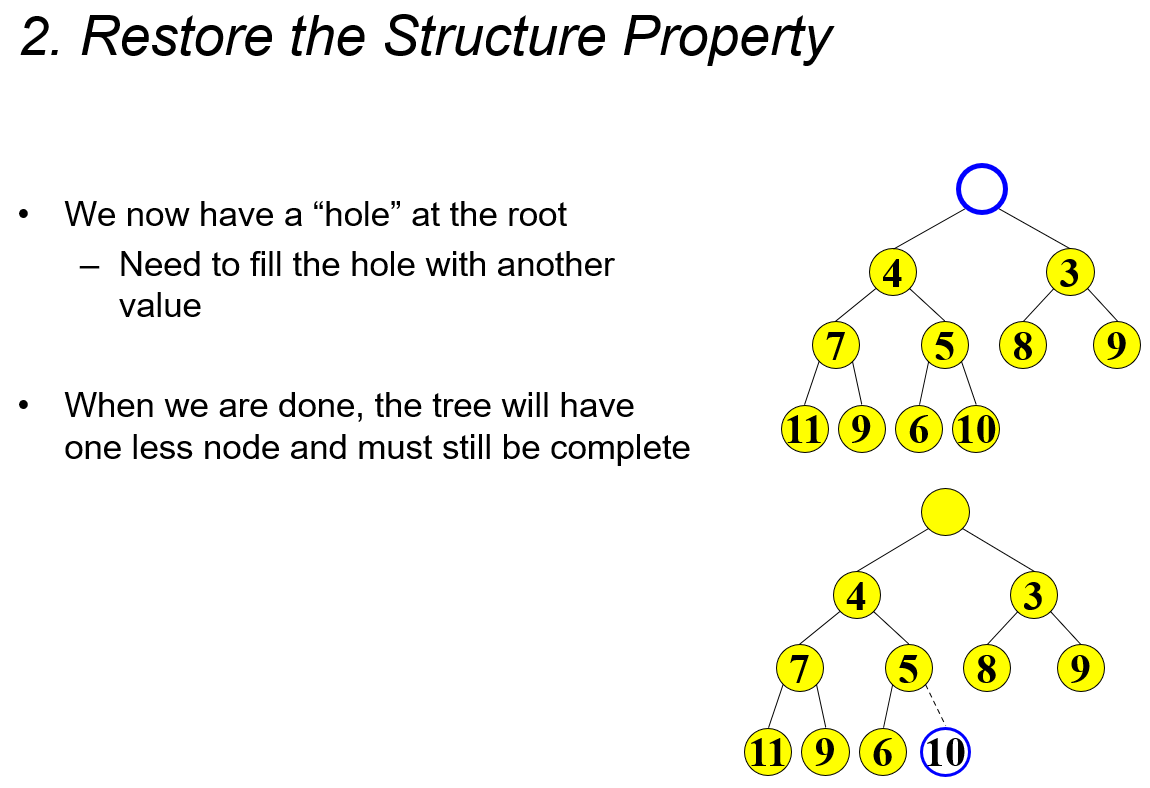
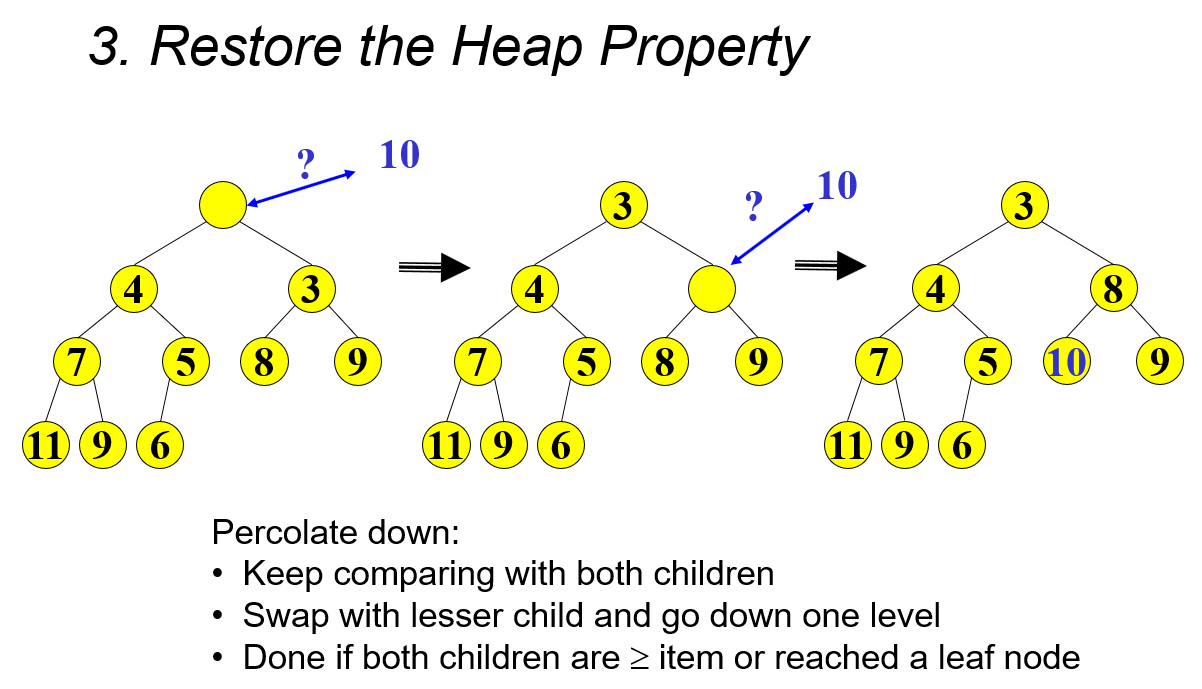
- Run time is O(height of heap)
- A heap is a complete binary tree
- Height of a complete binary tree of n nodes?
- height = \(\log_2(n)\)
- Run time of
removeMinis \(O(\log n)\)
4.1.2 add

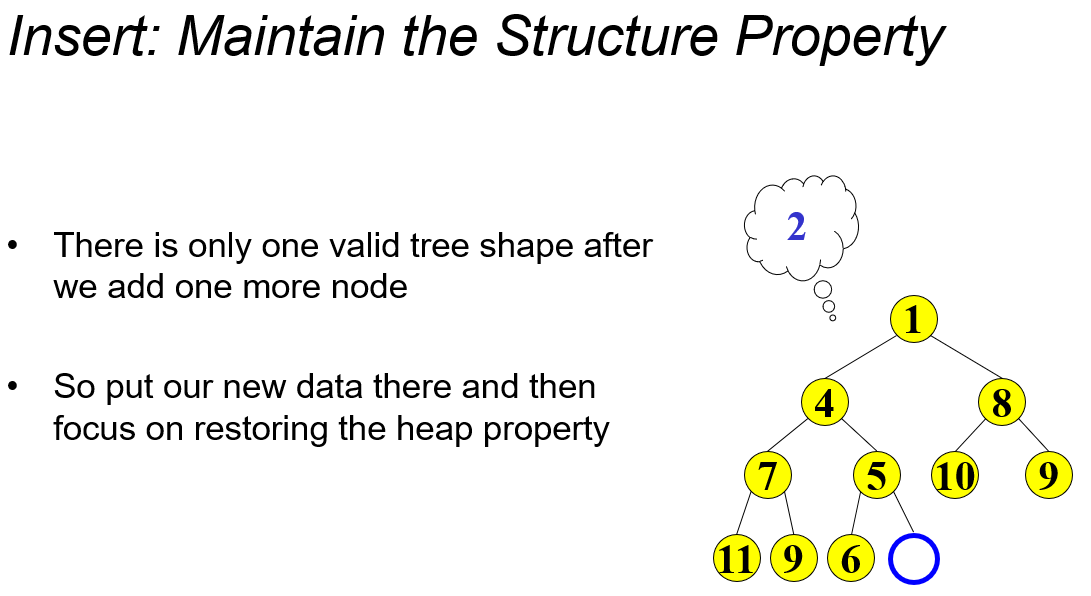
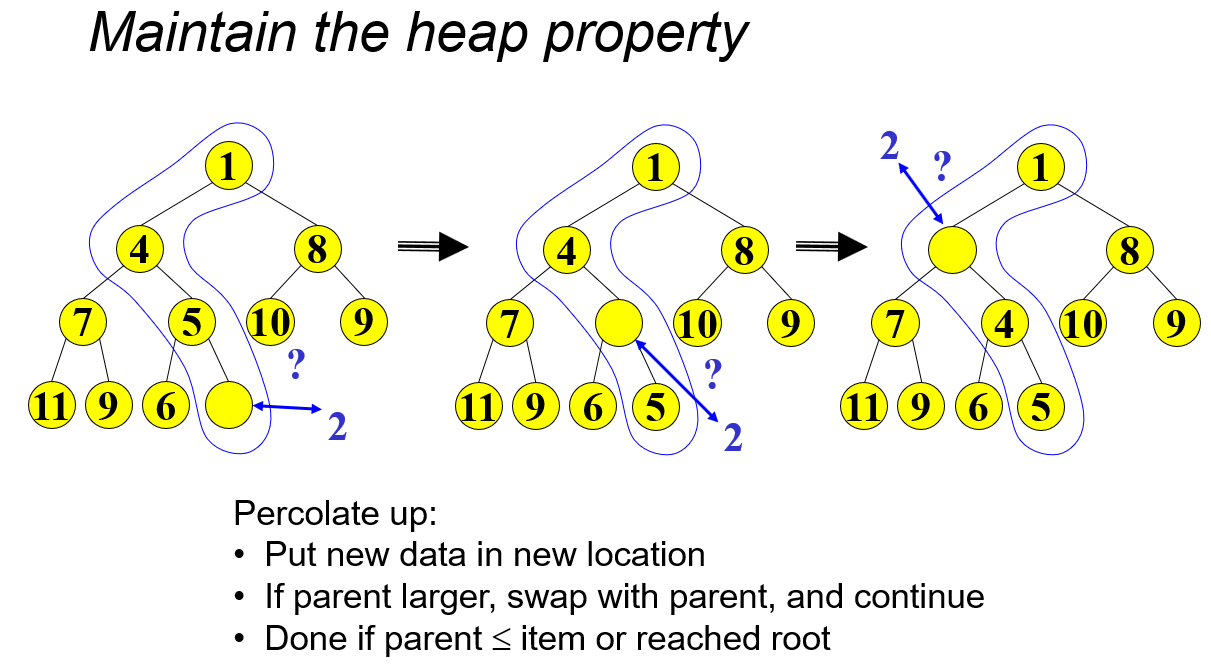
- Like
removeMin, worst-case time proportional to tree height- \(O(\log n)\)
- But there's a problem:
removeMinneeds to know the right-most node in the bottom row, andaddneeds to know the first empty spot in the bottom row- If "keep a reference to there" then
addandremoveMinhave to adjust that reference: \(O(\log n)\) in worst case - Could calculate how to find it in \(O(\log n)\) from the root given the size of the heap
- But it's not easy
- And then
addis always \(O(\log n)\), promised \(O(1)\) on average (assuming random arrival of elements)
- If "keep a reference to there" then
- There's a trick: don't represent complete trees with explicit edges!
4.2 Animations
5 Array Representation of Binary Trees
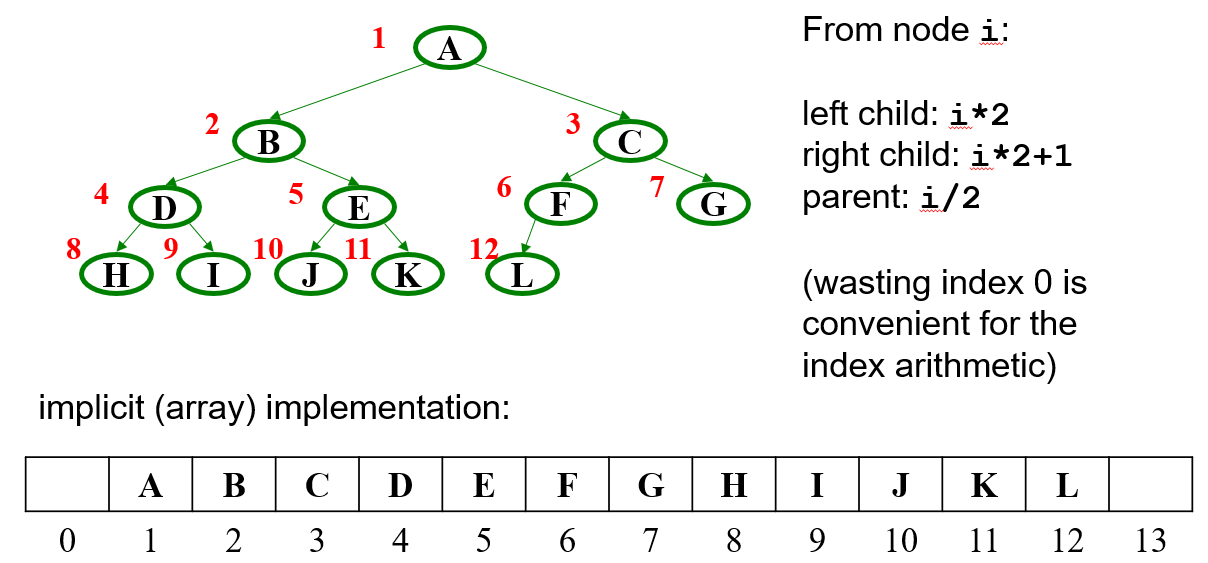
- Pros:
- Non-data space: just index 0 and unused space on right
- In conventional tree representation, an average of one edge per node (leaves have 0, interior have 1 or 2), so linear additional space required (like next/prev for linked lists)
- Array would waste more space if tree were not complete
- Multiplying and dividing by 2 is very fast (shift operations in hardware)
- Last used position is just index
size
- Non-data space: just index 0 and unused space on right
- Cons:
- Same might-be-empty or might-get-full problems we saw with stacks and queues (resize by doubling as necessary)
Pros outweigh cons: this is how people do it
5.1 Example
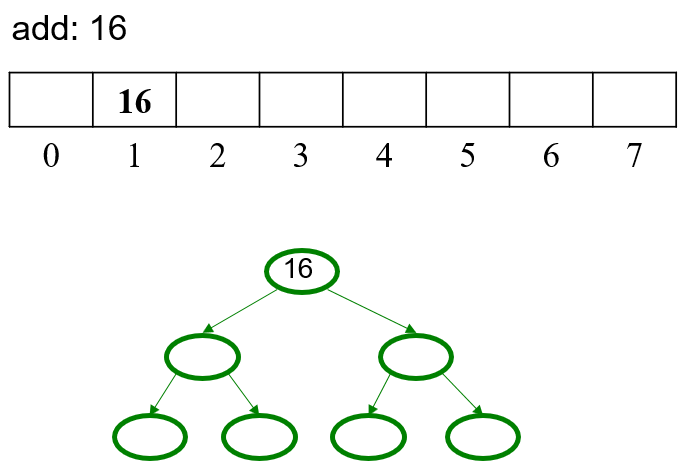
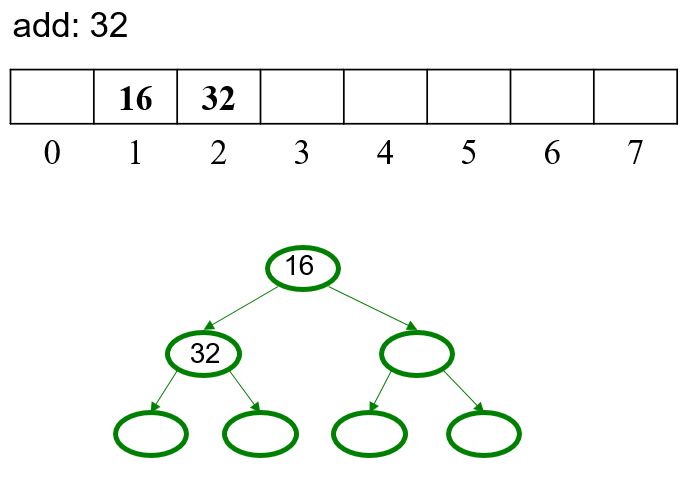
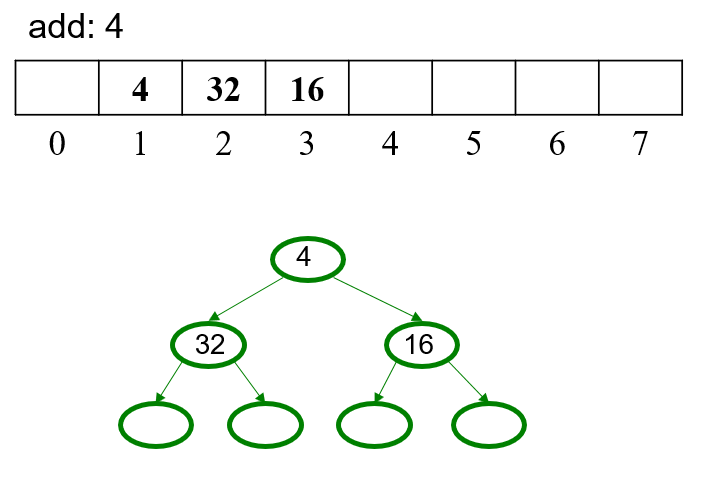
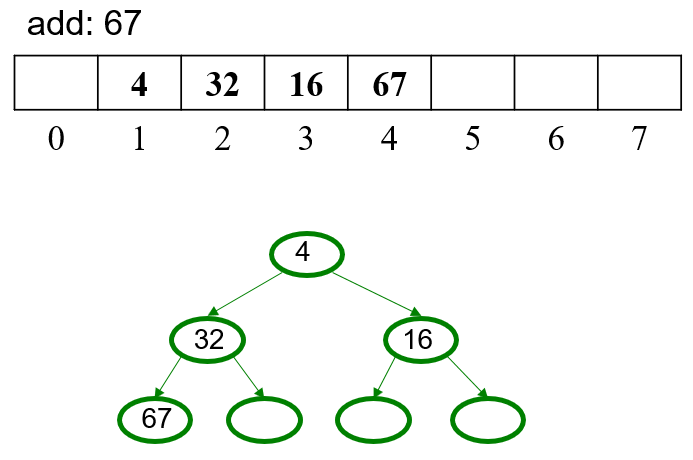
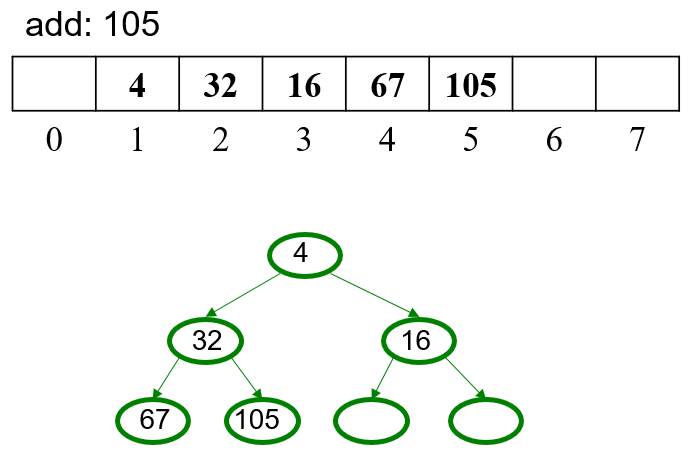
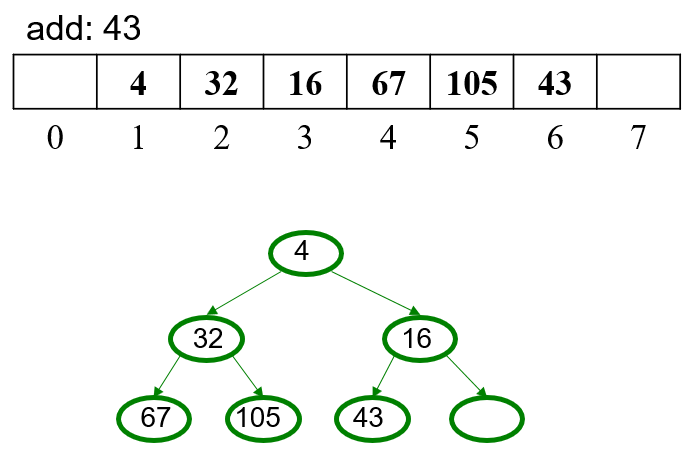
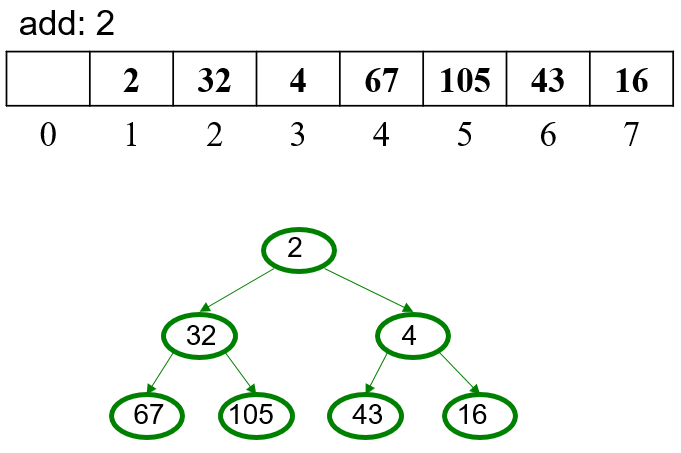
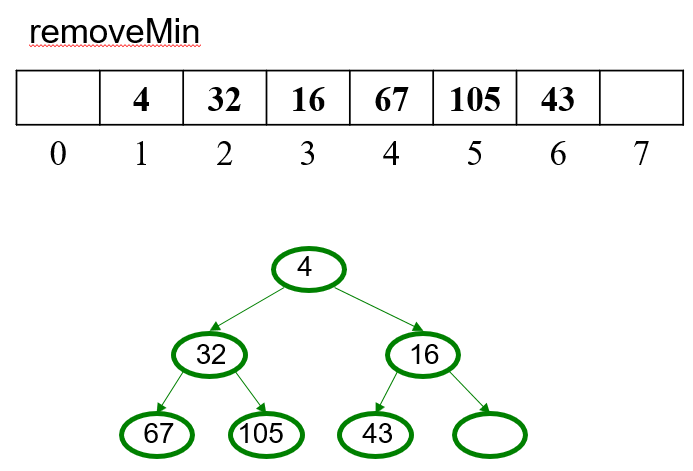
5.2 OPTIONAL Pseudocode

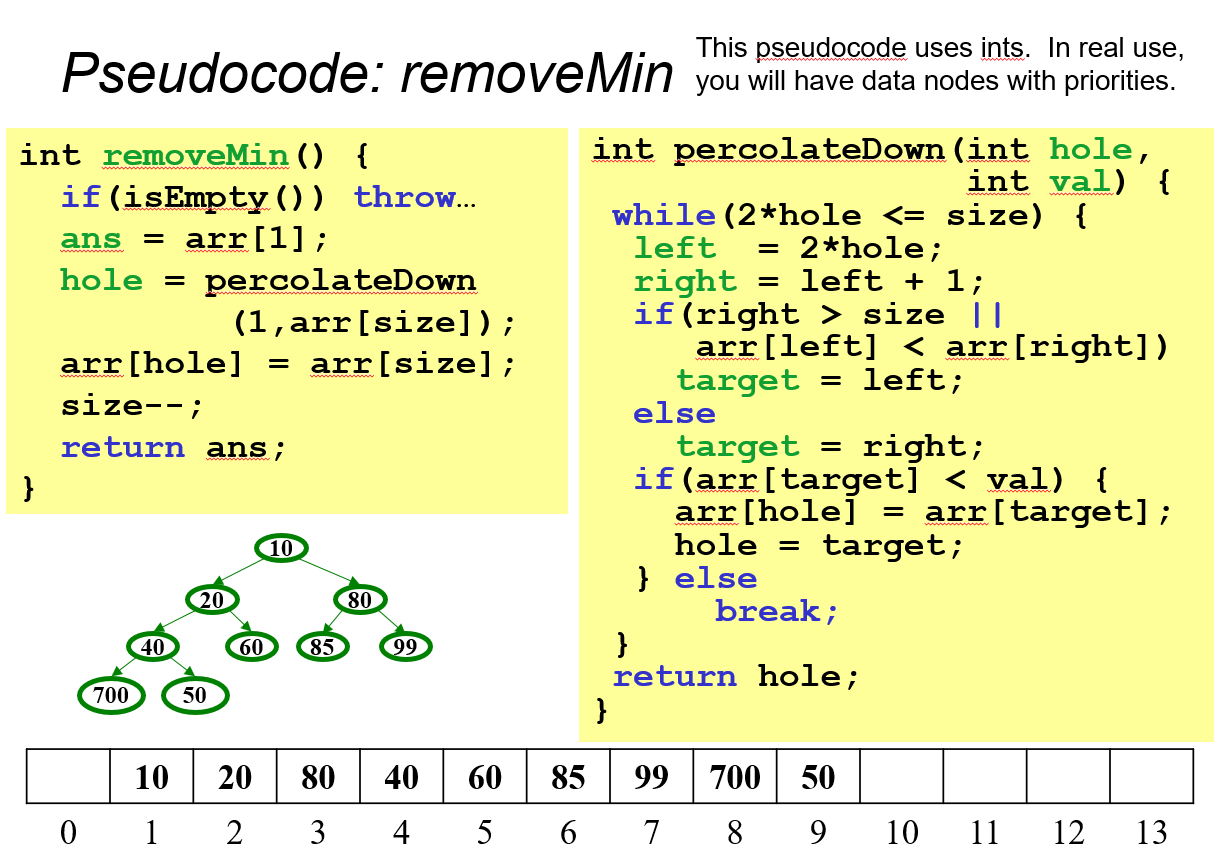
6 Exercise
- Starting with MinIntHeap.java, add and test two methods
- First is the
checkHeap()method, whose purpose is to ensure the heap property is followed (as a way of debugging/ensuring the implementation is correct)- Note how
checkHeapis called in the other methods—a "check" method like this is a great strategy for testing a data structure implementation - The method should check every parent-child pair
- If a parent is greater than a child,
throw new RuntimeException("HELPFUL MESSAGE GOES HERE");Arrays.toString(heap)will produce a string version of the heap array
- The provided
addandremoveMinmethods are correct, so running the initialmainmethod should not cause any exceptions - Switch to the other
mainmethod: running that should cause an exception because it uses the constructor that takes an array to use as the initial heap - Since this constructor does nothing to ensure the array is a valid heap,
checkHeapshould catch a problem
- Note how
- Second is the
MinIntHeap(int[] input, int size)constructorinputis a binary tree represented using an array, but not one that necessarily observe the heap property- The constructor should heapify the array, percolating appropriately to enforce the heap property
This is essentialy problem 13.10 from Bailey:
Reconsider the "heapifying" constructor discussed in Section 13.4.2. Instead of adding \(n\) values to an initially empty heap (at a cost of \(O(n \log n)\)), suppose we do the following: Consider each interior node of the heap in order of decreasing array index. Think of this interior node as the root of a potential subheap. We know that its subtrees are valid heaps. Now, just push this node down into its (near-)heap.
- Use the
checkHeapyou just wrote to help you debug this constructor - Once you think it's working, increase the size of
inputto make sure
- My solution: MinIntHeapExtended.java
7 Practice Problems1
- Which of the following statements about min-heaps is true?
- Smaller values are on the left and larger values are on the right.
- The smallest value is the root.
- The smallest value is one of the leaves.
- Every value is smaller than all values at lower levels of the tree. For example, if there is a 25 at level 3, there will not be any elements with values less than 25 at levels 4 and beyond.
- If a binary heap has 26 nodes, what is its height? If it has 73 nodes, what is the height? How do you know for sure?
- Draw the tree for the binary min-heap that results from inserting 4, 9, 3, 7, 2, 5, 8, 6 in that order into an initially empty heap.
- Perform 3 removals on the heap you drew in the previous problem. Show the complete state of the tree after each removal.
- Draw the state of the array for an array-based min-heap after each of the values 3, 4, 7, 0, 2, 8, and 6 are added, in that order.
- Draw the tree version of a min-heap being represented by the given array:

Footnotes:
Solutions:
- The smallest value is at the root is true.
- If a binary heap has 26 nodes, its height is 5. If it has 73 nodes, its height is 7. We know for sure because every heap is a complete tree, so its shape and height are predictable given its size. The height of a heap of size N will always be equal to \(\log_2 N\), rounded up.
The resulting binary min-heap after all adds is the following:
2 / \ 3 4 / \ / \ 6 7 5 8 / 9The resulting binary min-heap after each of the three removals is the following. After first removal:
3 / \ 6 4 / \ / \ 9 7 5 8After second removal:
4 / \ 6 5 / \ / 9 7 8After third removal:
5 / \ 6 8 / \ 9 73, 4, 7, 0, 2, 8, and 6
+---+---+ | | 3 | +---+---+ +---+---+---+ | | 3 | 4 | +---+---+---+ +---+---+---+---+ | | 3 | 4 | 7 | +---+---+---+---+ +---+---+---+---+---+ | | 0 | 3 | 7 | 4 | +---+---+---+---+---+ +---+---+---+---+---+---+ | | 0 | 2 | 7 | 4 | 3 | +---+---+---+---+---+---+ +---+---+---+---+---+---+---+ | | 0 | 2 | 7 | 4 | 3 | 8 | +---+---+---+---+---+---+---+ +---+---+---+---+---+---+---+---+ | | 0 | 2 | 6 | 4 | 3 | 8 | 7 | +---+---+---+---+---+---+---+---+
Heap represented by the given array:
29 / \ 41 30 / \ / \ 55 68 37 41 / 80