CS 208 f21 — Programming With Bits
Table of Contents
1 bitwise operators
A bitwise operator is a mathematical operator the works at the level of bits. In particular these operators act on each bit of the input separately. These operations closely resemble the actual circuitry that make up computer components. Those circuits take in one or two electrical signals at either a high (1) or low (0) voltage, and output a high or low voltage (a 1 or a 0).
This correspondence between circuitry and these operators often makes them faster and/or more power efficient than standard arithmetic operations. Thus, compilers tend to use them in place of standard arithmetic when possible.
To demonstrate these different operations, we'll define two bit vectors A and B each 8 bits long.
A bit vector (also called a bit array or bit string) is a string of zeros and ones of some fixed length.
A=11101001B=01010101
1.1 bitwise AND
&represents bitwise AND- AND takes two bits and produces a 1 if both inputs are 1, otherwise it produces 0
A & B:
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|
| & | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
1.2 bitwise OR
|represents bitwise OR- OR takes two bits and produces a 1 if either inputs are 1, otherwise it produces 0
A | B:
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|
| | | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
1.3 bitwise XOR (eXclusive OR)
^represents bitwise XOR- XOR takes two bits and produces a 1 if either, but not both inputs are 1, otherwise it produces 0
A ^ B:
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|
| ^ | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
1.4 bitwise NOT
~represents bitwise NOT- NOT takes one bit and produces the inverse of its input (i.e., it flips the bit, 0 to 1 and 1 to 0)
~B:
| ~ | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
Bitwise NOT can be used to derive a formula for negation (additive inverse) in two's complement:
x + ~x = 0b11...11(if we sumxand~xwe get a binary number that's all 1s since~xhas a 1 everywherexhas a 0 and vice versa)x + ~x = -1(all 1s represents -1 in two's complement for any width)x + ~x + 1 = 0(add 1 to both sides)~x + 1 = -x(subtractxfrom both sides—to get the additive inverse of a two's complement number, apply bitwise NOT and add 1)
2 bit shifting
Bit shift operators are slightly different from the four bitwise operators we've looked at so far. Instead of operating on each individual bit or pair of bits in place, they slide the bits \(n\) places to the left or right.
2.1 left shift
<<represents left shift- left shift takes a bit vector and an integer \(n\) and shifts the bits \(n\) places to the left, filling in with zeros
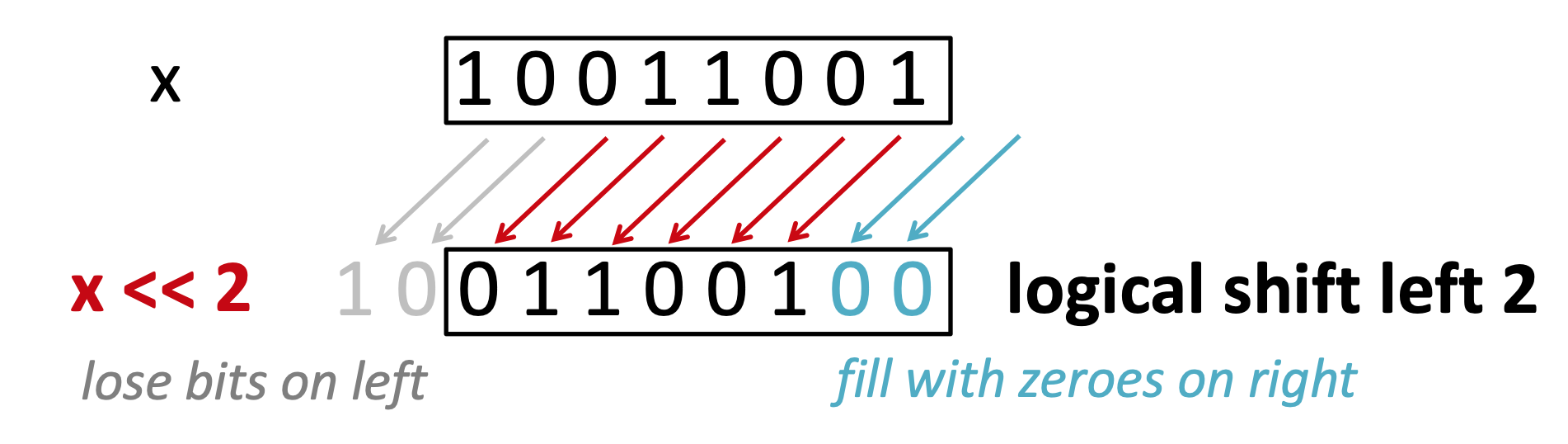
A<<1:
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | _ |
| _ | 1 | 1 | 0 | 1 | 0 | 0 | 1 | _ |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
2.2 right shift
>>represents right shift- right shift takes a bit vector and an integer \(n\) and shifts the bits \(n\) places to the right
- a logical right shift fills in with zeros
- a arithmetic right shift fills in with copies of the most significant bit
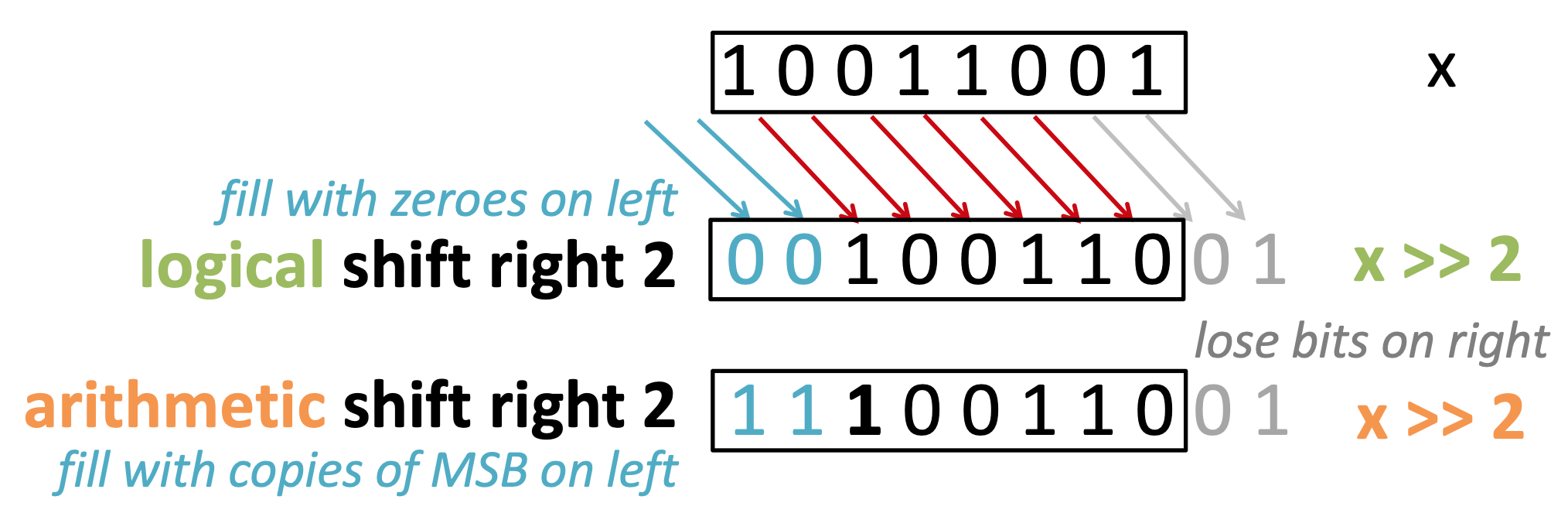
A>>1(logical):
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | ||
|---|---|---|---|---|---|---|---|---|---|
| _ | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | |
| _ | 1 | 1 | 1 | 0 | 1 | 0 | 0 | _ | |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
A>>1(arithmetic):
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | ||
|---|---|---|---|---|---|---|---|---|---|
| _ | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | |
| _ | 1 | 1 | 1 | 0 | 1 | 0 | 0 | _ | |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
3 Boolean operators
C also provides logical operators for and, or, and not.
These are written &&, ||, and ! in C.
They treat 0 as representing false and any other value as representing true.
They return either 0 or 1, indicating a logically false or true expression, respectively.
| Expression | Result |
|---|---|
!0x41 |
0x00 |
0x55 && 0x00 |
0x00 |
0x55 || 0x00 |
0x01 |
If shifting a base 10 number one place to the left multiplies by 10 and one place to the right divides by 10, what does shifting a binary number do to its value?1
4 Bitwise operations in C
- in C, these operators can apply to any integral data type
- 1-byte (
char) examples (verify you understand how these work):2~0x41~0x000x68 & 0x550x68 | 0x550x34<<10x68>>2!0x00!!0x41~(0x00 || !0x20)- how many bits are in each of these results?
- all of them contain 8 bits (1 byte)! zeroes used to "fill out" the fixed length
- 1-byte (
5 Packing and Extracting
These operations are also essential in settings with very little memory.
Since storage sizes are fixed, like a 4-byte integer, representing 1-bit of information like true/false (1 or 0) will leave a lot of space unused.
To be more efficient, we might want to combine a bunch of values into the bits of an int, with each value using a different range of the 32 bits.
We would need ways of combining and extracting these values, however, and that's where bitwise operators come in.
Returning to the idea of combining multiple values into a single quantity, let's say we want to store three 1-byte characters in a 4-byte integer.
The code below shows how these quantities would be combined and extracted.
All the types are unsigned to prevent C from performing sign extension when converting a char to an int.
#include <stdio.h> int combine(unsigned char a, unsigned char b, unsigned char c) { unsigned result = a; // result has a in the low order byte, 0 in the rest printf("result = %x\n", result); result = (result<<8) | b; // shift a 1 byte to the left, use OR to put b in the low order byte printf("result = %x\n", result); result = (result<<8) | c; // shift a and b 1 byte to the left, use OR to put c in the low order byte printf("result = %x\n", result); return result; } int main() { unsigned char a = 0xaa; unsigned char b = 0xbb; unsigned char c = 0xcc; unsigned x = combine(a, b, c); // use the shift-and-mask strategy to extract each char // masking means use AND to zero-out bits you don't care about, leaving only the ones you do printf("a = %x\n", (x>>16) & 0xff); // shift x to the right to put a in low byte, mask out the rest with AND printf("b = %x\n", (x>>8) & 0xff); // shift x to the right to put b in low byte, mask out the rest with AND printf("c = %x\n", x & 0xff); // c is already in the low byte, mask out the rest with AND }
QUICK CHECK: write a C expression to extract most significant byte from a 32-bit integer3.
For example, given x = 0b 01100001 01100010 01100011 01100100 (spaces added to separate bytes), should return 0b 00000000 00000000 00000000 01100001
6 Pracice
CSPP practice problems 2.12 (p. 55), 2.14 (p. 57), 2.15 (p. 57), and 2.16 (p. 58)
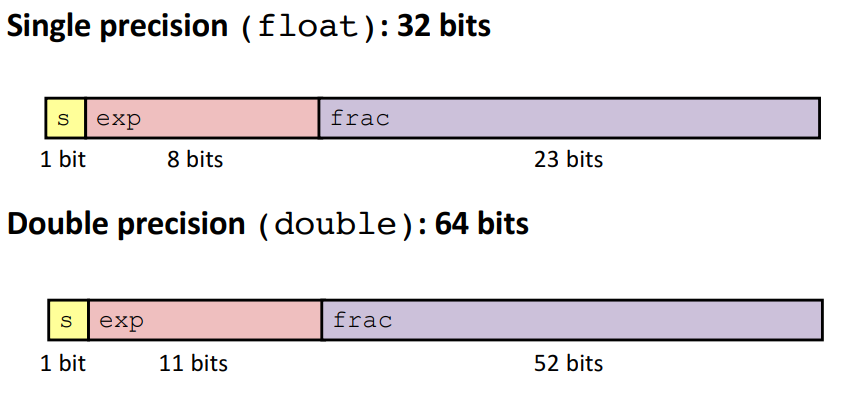
7 IEEE-754 Floating Point

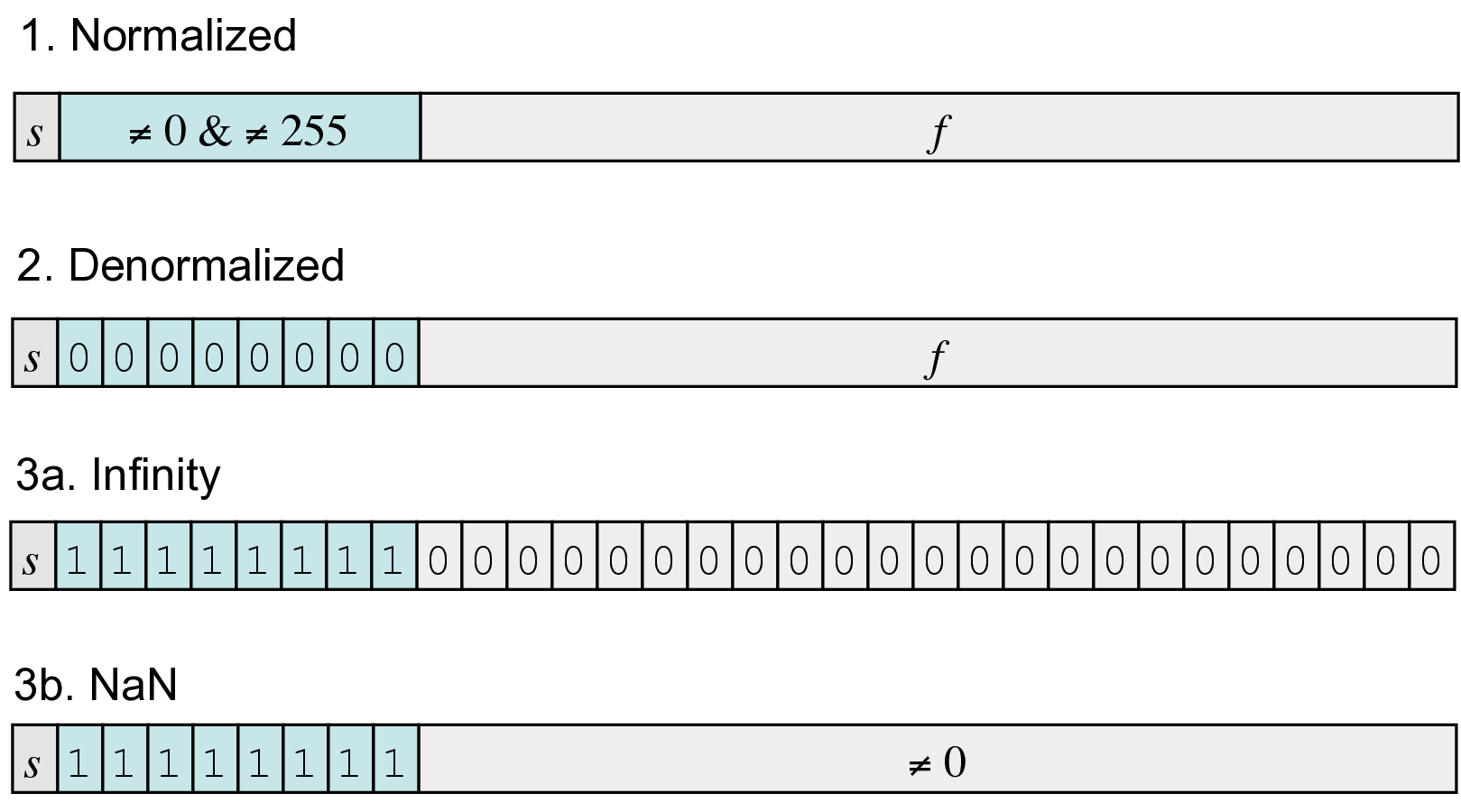
7.1 Special cases
8 Useful simulation
9 Arithmetic
- IEEE standard specifies four rounding modes
- typically round-to-even, helps avoid statistical bias in practice by distributing rounding between rounding up and rounding down
- In general, perform exact computation and then round to something representable with available bits
- can underflow if closest representable value is 0
- can overflow if \(E\) is too big to fit in
exp(result is \(\pm\infty\)) - rounding breaks associtivity
Footnotes:
Shifting 1 to the left multiplies by 2, shifting 1 to the right divides by 2
~0x41\(\rightarrow\)~0b01000001\(\rightarrow\)0b10111110\(\rightarrow\)0xbe~0x00\(\rightarrow\)0xff0x68 & 0x55\(\rightarrow\)0x400x68 | 0x55\(\rightarrow\)0x7d0x34<<1\(\rightarrow\)0x680x68>>2\(\rightarrow\)0x1a!0x00\(\rightarrow\)0x01!!0x41\(\rightarrow\)0x01~(0x00 || !0x20)\(\rightarrow\)~(0x00 || 0x00)\(\rightarrow\)~0x00\(\rightarrow\)0xff- how many bits are in each of these results?
- all of them contain 8 bits (1 byte)! zeroes used to "fill out" the fixed length
Use shift-and-mask: (x>>24) & 0xff