CS 208 f21 — Integer Arithmetic

Table of Contents

1 Warmup

What base-10 integers do these 8-bit quantities represent using two's complement?

  • 0b00001001 = 9
  • 0b10000001 = -127

2 Two's Complement Arithmetic

  • the same procedure works for both unsigned and two's complement addition
    • add the bits as you would expect, discard any that carry out of the most significant bit
      • example: \(4 + (-3)\) = 0100 + 1101 = 10001 = 0001 = \(+1\)
  • this is handy because it means the same hardware can perform both signed and unsigned addition

3 Overflow

  • Overflow occurs when the result of a computation can't be represented by the current encoding
  • For example, \(6 + 3\) = 0110 + 0011 = 1001 = \(-7\)
    • The expected result of \(6+3=9\) exceeds the range of positive numbers 4-bit two's complement can represent

3.1 Fixed-width arithmetic is modular

When we have a fixed number of bits (e.g., 4-bit two's complement), arithmetic becomes modular.

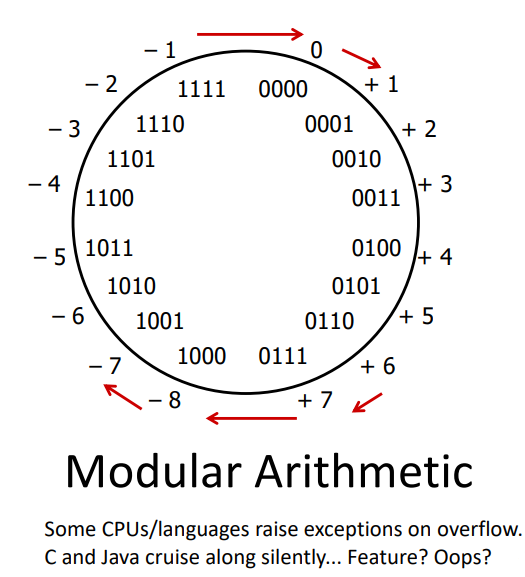
twos-complement-modular.png

The result of an addition is the sum modulo \(2^w\) (in raw binary—it's then up to the program whether the result is interpreted as signed or unsigned). Intuitively, think of fixed-width arithmetic as wrapping around when it goes too positive or too negative. With 4-bit two's complement, subtract 1 from -8 and it overflows to +7. Similarly, add 1 to +7 and it overflows to -8.

Here we finally see why int x = 200 * 300 * 400 * 500 results in a large negative value. The result of the multiplication overflows the largest positive value than can be represented by a 32-bit int and wraps around into negative values.

4 Sign Extension

When converting signed integer to a larger integral type, extend with copies of the most significant bit (i.e., sign bit)

  • 4-bits to 8-bits:
    • 5 goes from 0101 to 00000101 (still 5)
    • -5 goes from 1011 to 11111011 (still -5)
  • Called sign extension because we maintain the same value by extending the sign bit to fill in the new bits
    • This is what C will do if you cast a smaller signed integer type to a larger one (i.e., cast an int to a long)
    • Casting unsigned types does not perform sign extension, the new bits are filled with zeros (zero extension).

5 Truncation

One the other hand, going from a larger integer type to a smaller one just throws away (truncates) the extra bits.

  • 8-bits to 4-bits:
    • 23 goes from 00010111 to 0111 (now 7)
    • -23 goes from 11101001 to 1001 (now -7)

6 Two's Complement Arithmetic Practice

Verify that binary addition produces the correct two's complement result for these expressions:1

  • \(-2 + -3\)
  • \(2 + -3\)

6.1 Additive inverse

Important that for all \(x\), the bit representation of \(x\) and the bit representation of \(-x\) sum to 0 (\(mod\ 2^w\)). That is, it had better be the case that \(x + (-x) = 0\) (throwing away any bits that carry out off the left side) Find the 8-bit negative encodings for these three bit vectors and verify that the sum of the two is 0:2

  • 0b00000001
  • 0b00000010
  • 0b11000011

Additive inverses are well behaved for two's complement. We'll see how to quickly find the additive inverse in binary in Friday's topic.

7 Sign Extension

Which of the following 8-bit numbers has the same signed (2's complement) value as the 4-bit number 0b1100?3 (spaces added for readability)

  • 0b 0000 1100
  • 0b 1000 1100
  • 0b 1111 1100
  • 0b 1100 1100

8 Practice

  1. CSPP practice problems 2.25 and 2.26
    • These highlight the practical application of understanding integer representations
  2. CSPP practice problem 2.29 (p. 93)
    • They use \(+\) to mean "normal" addition (not modular) and \(+_5^t\) to mean 5-bit two's complement addition
    • The case refers to the for possibilities in Figure 2.24
      1. \(x + y\) is negative and \(x +_5^t y\) overflows to a positive result
      2. \(x + y\) is negative and \(x +_5^t y\) does not overflow (also negative)
      3. \(x + y\) is positive and \(x +_5^t y\) does not overflow (also positive)
      4. \(x + y\) is positive and \(x +_5^t y\) overflows to a negative result

Footnotes:

1

Verify binary addition produces the correct result:

  • \(-2 + -3 =\) 0b1110 + 0b1101
  1 1 1 0
+ 1 1 0 1
1 1 0 1 1
_ 1 0 1 1

final result: 0b1011 = \(-5\)

  • \(2 + -3 =\) 0b0010 + 0b1101
  0 0 1 0
+ 1 1 0 1
  1 1 1 1

final result: 0b1111 = \(-1\)

2

Find the additive inverses, verify the sum is 0:

  • 0b00000001 = 1, inverse is \(-1\) = 0b11111111
  1 1 1 1 1 1 1 1
+ 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0
_ 0 0 0 0 0 0 0 0
  • 0b00000010 = 2, inverse is \(-2\) = 0b11111110
  1 1 1 1 1 1 1 0
+ 0 0 0 0 0 0 1 0
1 0 0 0 0 0 0 0 0
_ 0 0 0 0 0 0 0 0
  • 0b11000011 = \(-61\), inverse is \(61\) = 0b00111101
  1 1 0 0 0 0 1 1
+ 0 0 1 1 1 1 0 1
1 0 0 0 0 0 0 0 0
_ 0 0 0 0 0 0 0 0
3

What is the 8-bit equivalent of 0b1100 (\(-4\))

  • 0b 0000 1100 is 12
  • 0b 1000 1100 is \(-116\)
  • 0b 1111 1100 is \(-4\) (correct answer)
  • 0b 1100 1100 is \(-52\)