CS 208 f21 — Integer Representation
Table of Contents
1 Review
2 Memory Layout
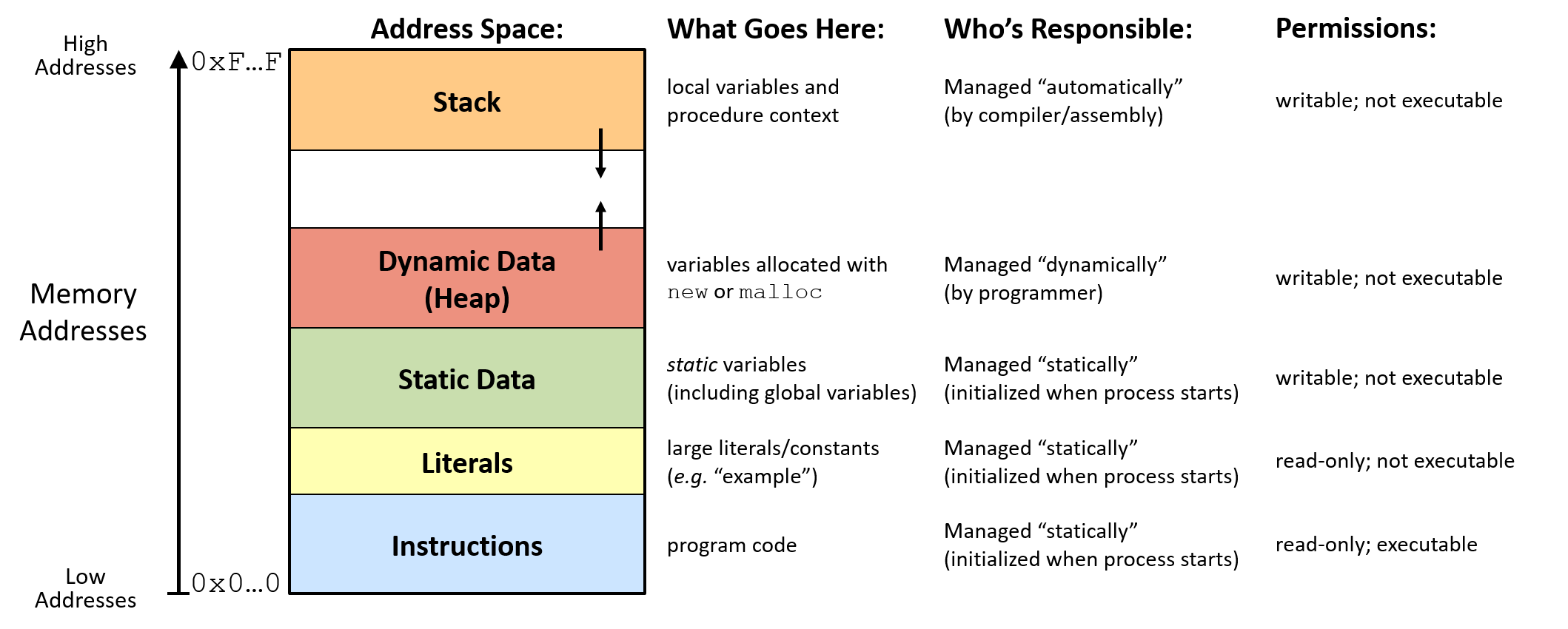
Though memory is a long array of bytes, it is actually separated into various segments or memory regions. Memory allocated at compile time is located on the stack, which resides at high addresses in memory. As more data is added to the stack, the region grows to include lower addresses, so we say the stack grows down.
Memory allocated dynamically using malloc is placed on the heap, which resides somewhere in the middle of memory.
As more data is added to the heap, the region grows to include higher addresses, so we say the heap grows up.
The other three regions (static data, literals, and instructions) are fixed in size and get initialized when a program starts running.
3 Dynamic Memory Allocation
- We can dynamically allocate storage space while the program is running, but we cannot create new variable names "on the fly"
- For this reason, dynamic allocation requires two steps:
- Creating the dynamic space.
- Storing its address in a pointer (so that the space can be accesed)
- To dynamically allocate memory in C, we use the
mallocfunction provided bystdlib.hmalloctakes in a number of bytes to allocate and returns a pointer to the newly allocated spacemallocdoes not do any initialization, so the contents of this memory can be whatever was last written to those bytes- this means you must always perform initialization on memory return by
malloc
- this means you must always perform initialization on memory return by
- De-allocation:
- Deallocation is the "clean-up" of space being used for variables or other data storage
- Compile time variables are automatically deallocated based on their known extent
- It is the programmer's job to deallocate dynamically created space
- To de-allocate dynamic memory, we use the
freefunction operatorfreetakes a pointer that was previously returned bymallocand makes that memory available for future allocationfreehas undefined behavior is used with a pointer that wasn't returned bymallocor a pointer that was already freed
4 C Review
Practice your what you've been learning about C by finding the the problems with the code below. I've noted the lines where compiler errors occur—try and figure out how you would resolve them. Once those are fixed, there are two potential run-time errors. These may crash the program, or not affect it at all (ah, the fun of working closely with memory in C). See if you can spot them, and then check your thinking at the end of these notes3.
#include <stdlib.h> #include <string.h> typedef struct node { struct node *left; struct node *right; char *value; } node_t; int main() { char *s = "noodles"; node_t *root = (node_t*) malloc(node_t); // gcc error: expected expression before ‘node_t’ if (*root == NULL) { // gcc error: invalid operands to binary == (have ‘node_t {aka struct node}’ and ‘void *’) return 1; } *root->left = NULL; // gcc error: incompatible types when assigning to type ‘struct node’ from type ‘void *’ *root->right = NULL; // gcc error: incompatible types when assigning to type ‘struct node’ from type ‘void *’ root->value = (char*) malloc(sizeof(char)); strcpy(root->value, s); free(root); free(root->value); }
5 Integer Representation
Recall the example from the first topic where 200 * 300 * 400 * 500 resulted in -884901888?
Over the next two topics studying how integers are represented on computer systems, we will see why exactly this happens.
5.1 Why study this low-level implementation detail?
At first, integer representation may seem like a low-level detail that programmers never have to think about in practice. Why then is it worthwhile to understand deeply? Two main reasons:
- Because a vital part of your education at Carleton in general and in courses like 208 specically is looking inside of things and understanding why and how they work. We won't be satisfied with just waving our hands and saying "some arrangement of bits in memory make integers happen, don't worry about it." We'll take this opportunity to deepen our knowledge and see a great example of the concept of an encoding—a set of rules that translate a group of things, in this case integers, into bits.
- And because situations where it matters arise in practice and getting it wrong can have very serious consequences
- In 1996 an expensive European Space Agency rocket exploded due to a software crash caused by converting a 64-bit floating point number to a 16-bit signed integer.
- In 2015, it was found that Boeing 787 Dreamliners contained a software flaw, very likely caused by signed integer overflow, that could result in loss of control of the airplane
5.2 bit weight
The way integers are represented involves the concept of a bit's weight.
This just means the value that bit contributes to the overall value of a set of bits.
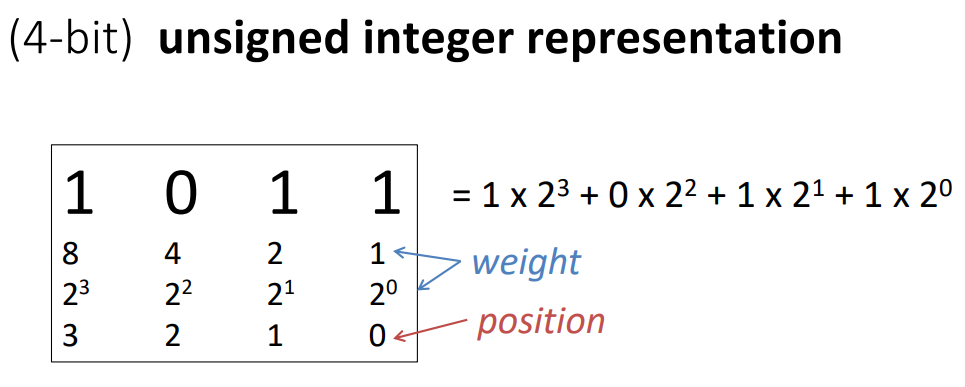
For example, the binary number 0b0101 corresponds to 5 in decimal.
There are 1s in the 1s place and the 4s place, giving us \(1 + 4 = 5\).
We would say the rightmost 1 has a positive weight of 1 and the other 1 has a positive weight of 4.
Stated in a more mathematical way: consider a bit vector \(x\) of width \(w\) with bits \([x_{w-1},x_{w-2},\ldots,x_0]\). When interpreting \(x\) as an integer, we will refer to the value a particular bit contributes as its weight. Usually, the weight of each bit just corresponds to the value it would have in a binary number (i.e., bit \(x_i\) has a weight of \(2^i\))
6 Unsigned Integers
To start with the simpler case, let's look at unsigned integers. Though no type in C uses only 4 bits, I'll be using 4-bit representations to introduce integer concepts. Fewer bits will make it easier to see what's going on and do quick practice problems.
For unsigned integers, we will count each bit as its positive weight. Below are all 16 4-bit unsigned integers in decimal and binary:
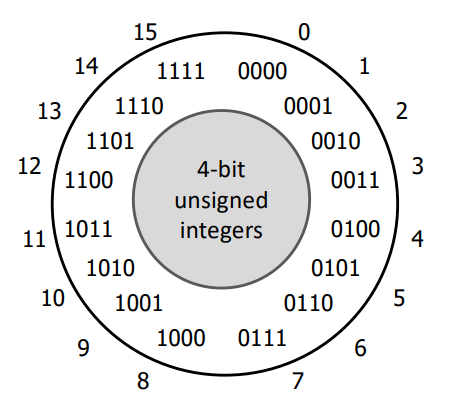
Think about what should happen if we add 1 to 0b1111.
Remember we only have 4 bits to work with.
You'll see what computers actually do in Wednesday's topic.
7 Signed Integer Representation as a Design Problem
Consider the two following possibilities for a 4-bit signed integer representation:
- sign and magnitude: the most significant bit indicates positive (0) or negative (1), the other bits count as their weight
0b0011would be 3,0b1011would be -3
- two's complement: the most significant bit counts as its negative weight (-8), the other bits count as their positive weight
0b0011would be 3,0b1101would be -3 (\(-8 + 4 + 1 = -3\))- why "two's complement"? Comes from the fact that \(-n\) is represented as the difference of a power of 2 and \(n\), specifically \(2^w - n\)
- Can see this in
0b1101for -3: \(w = 4\) (4-bit-wide representation), \(2^4 - 3 = 16 - 3 = 13 =\)0b1101
- Can see this in
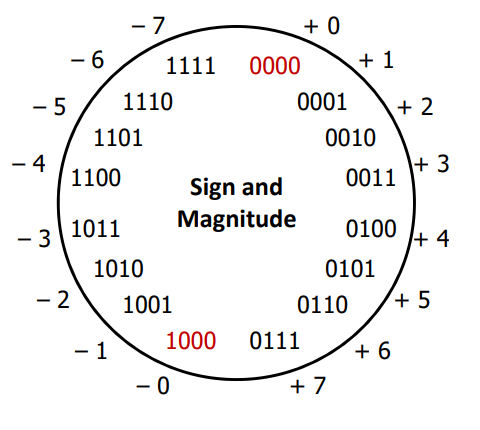
7.1 4-bit Sign and Magnitude
- two representations of zero (
0b0000and0b1000—negative zero??) - arithmetic is cumbersome as negatives "increment" in the wrong direction (i.e., adding 1 to a negative number makes it more negative)
7.2 4-bit Two's Complement
- negative numbers "flipped" so that incrementing does what we want
- no more -0
- preserves nice property of sign and magnitude that positive encodings match unsigned encodings
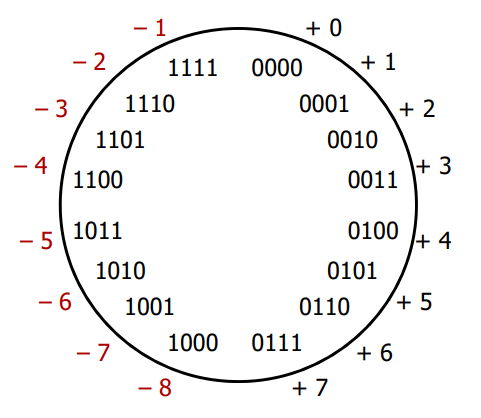
Note that the most significant bit end up still indicating the sign!
8 Quick Check
- Take the 4‐bit number encoding where
x = 0b1011 - Which of the following numbers is NOT a valid interpretation of
xusing any of the number representation schemes discussed in the video for today? (Unsigned, Sign and Magnitude, Two’s Complement) a. -4 b. -5 c. 11 d. -3
9 Practice
- CSPP practice problems 2.17 (p. 65) and 2.19 (p. 71)
- for 2.17, \(B2U_4\) means interpret the bits as 4-bit unsigned, \(B2T_4\) means interpret the bits as 4-bit two's complement
- for 2.19, \(T2U_4\) means convert from 4-bit two's complement to 4-bit unsigned
- Considering 8-bit integers4:
What is the largest integer?
Unsigned: Two's Complement: How do you represent (if possible) the following numbers: 39, -39, 127?
Unsigned Two's Complement 39:39:-39:-39:127:127:
It will be useful to have the powers of 2 at your fingertips as we go through this course, so here's a table of those
| \(n\) | \(2^n\) | \(n\) | \(2^n\) |
|---|---|---|---|
| 1 | 2 | 16 | 65536 |
| 2 | 4 | 17 | 131072 |
| 3 | 8 | 18 | 262144 |
| 4 | 16 | 19 | 524288 |
| 5 | 32 | 20 | 1048576 |
| 6 | 64 | 21 | 2097152 |
| 7 | 128 | 22 | 4194304 |
| 8 | 256 | 23 | 8388608 |
| 9 | 512 | 24 | 16777216 |
| 10 | 1024 | 25 | 33554432 |
| 11 | 2048 | 26 | 67108864 |
| 12 | 4096 | 27 | 134217728 |
| 13 | 8192 | 28 | 268435456 |
| 14 | 16384 | 29 | 536870912 |
| 15 | 32768 | 30 | 1073741824 |
Kilobyte (KB), megabyte (MB), and gigabyte (GB) refer to 210, 220, and 230 bytes respectively. They are also used to refer to 103, 106, and 109 bytes in some contexts.
Footnotes:
It would take 12 bytes: 11 characters at 1 byte each, plus the null terminator
struct point { int x; int y; };
#include <stdlib.h> #include <string.h> typedef struct node { struct node *left; struct node *right; char *value; } node_t; int main() { char *s = "noodles"; node_t *root = (node_t*) malloc(sizeof(node_t)); // use sizeof with the type to get the number of bytes if (root == NULL) { // compare the pointer to NULL (we want to check if malloc failed---it returns NULL in that case) return 1; } root->left = NULL; // we want to assign the pointer left itself to NULL // rather than writing NULL to the address it points to (what the * was doing) root->right = NULL; // we want to assign the pointer right itself to NULL root->value = (char*) malloc(sizeof(char)); // RUNTIME ERROR this allocates space for 1 char, // use malloc(strlen(s) + 1) * sizeof(char)) instead strcpy(root->value, s); free(root); free(root->value); // RUNTIME ERROR we are accessing root after freeing it, // this has undefined behavior (free root->value first, then free root) }
Considering 8-bit integers:
What is the largest integer?
Unsigned: Two's Complement: 255 127 How do you represent (if possible) the following numbers: 39, -39, 127?
Unsigned Two's Complement 39:0b0010011139:0b00100111-39: not possible-39:0b11011001127:0b01111111127:0b01111111