CS 208 f21 — Parallelism
1 Definitions
- concurrent computing: when the execution of multiple computations (or processes) overlap
- we need to correctly control access to shared resources
- parallel computing: when the execution of multiple computations (or processes) occur simultaneously
- using additional resources to produce an answer faster
- concurrency primarily about effective coordination, parallelism primarily about efficient division of labor
2 Why Parallelism?
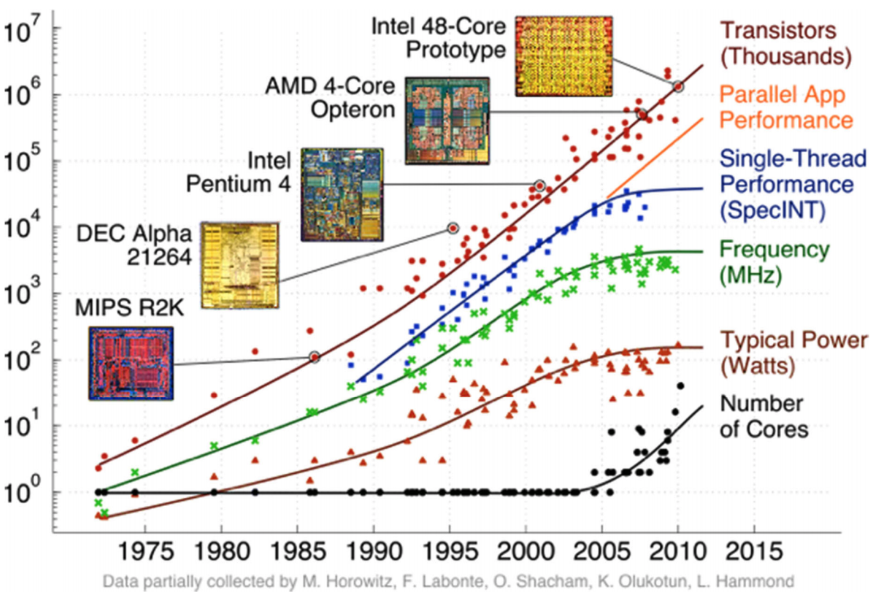
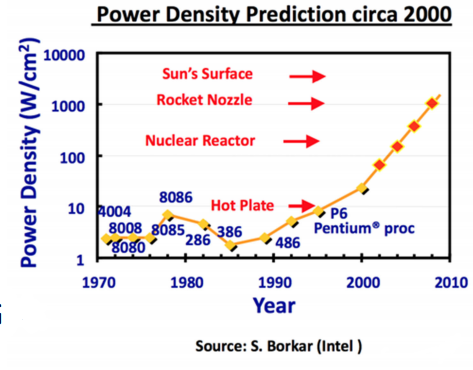
- running into physical limits:
- power densities over time roughly constant from 1958 to late 1990s
- grow rapidly starting in late 1990s
- Since 2000, transistors too small to shrink further (just a few molecules thick)
- power densities over time roughly constant from 1958 to late 1990s
- heat death
- power scales with frequency
- processors stopped around 4 GHz
- solution: slap multiple processors on a single chip
- continues the trend of more and more transitors, but…
- requires new programming approach

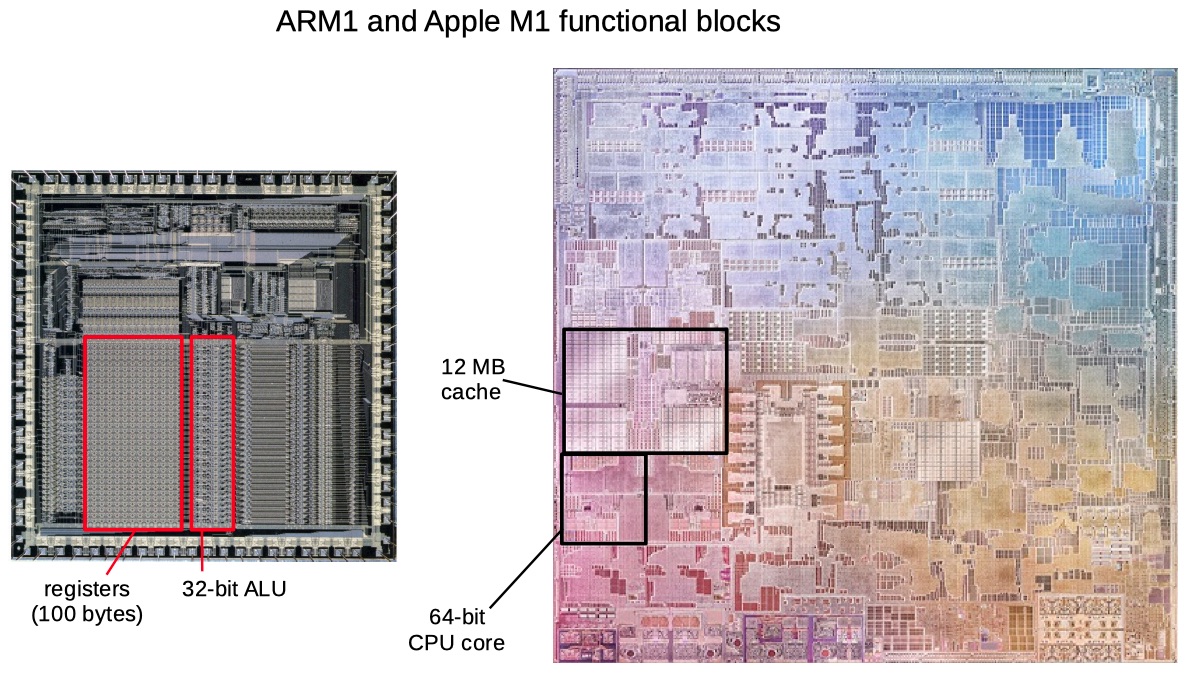
- First ARM processor created by Acorn Computers in 1985 for the BBC Micro computer vs Apple's recently announced M1 processor (also an ARM processor)
- ARM is an alternative processor architecture to the x86 architecture we've studied
- The M1 is over twice as large physically as the ARM1. It has 16 billion transistors vs 25,000 for the ARM1
- The ARM1 processor ran at 6 megahertz, while the M1 runs at 3.2 gigahertz, over 500 times faster
- While the ARM1 was a single processor, the M1 has 4 high-performance CPU cores, 4 efficiency CPU cores, a 16-core neural engine, and 8-core GPU
- Looking at the ARM1 die, you see functional blocks such as 100 bytes of registers and a basic 32-bit ALU. On the M1 die, similar-sized functional blocks are a 12-megabyte cache and a complete 64-bit CPU core.
- ALU = Arithmetic Logic Unit, the part of the processor that performs arithmetic
3 Parallel Sum
Global variables:
/* Single accumulator */ volatile data_t global_sum; /* Mutex for global sum */ pthread_mutex_t mutex; /* Number of elements summed by each thread */ size_t nelems_per_thread; /* Keep track of thread IDs */ pthread_t tid[MAXTHREADS]; /* Identify each thread */ int myid[MAXTHREADS];
Method #1: Accumulating in a global variable (where thread_fun is replaced with one of the two functions below)
nelems_per_thread = nelems / nthreads; /* Set global value */ global_sum = 0; /* Create threads and wait for them to finish */ for (i = 0; i < nthreads; i++) { myid[i] = i; Pthread_create(&tid[i], NULL, thread_fun, &myid[i]); } for (i = 0; i < nthreads; i++) Pthread_join(tid[i], NULL); result = global_sum; /* Add leftover elements */ for (e = nthreads * nelems_per_thread; e < nelems; e++) result += e;
Thread function with no synchronization:
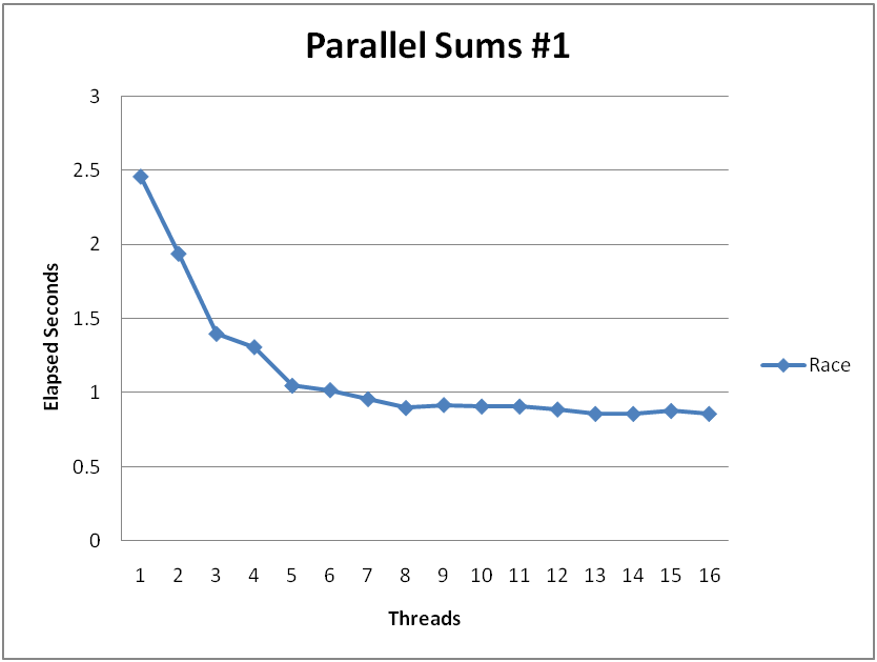
void *sum_datarace(void *vargp) { int myid = *((int *)vargp); size_t start = myid * nelems_per_thread; size_t end = start + nelems_per_thread; size_t i; for (i = start; i < end; i++) { global_sum += i; } return NULL; }
For \(N=2^{30}\): (gets wrong answer when > 1 thread)
Thread function using mutex:
void *sum_mutex(void *vargp) { int myid = *((int *)vargp); size_t start = myid * nelems_per_thread; size_t end = start + nelems_per_thread; size_t i; for (i = start; i < end; i++) { pthread_mutex_lock(&mutex); global_sum += i; pthread_mutex_unlock(&mutex); } return NULL; }
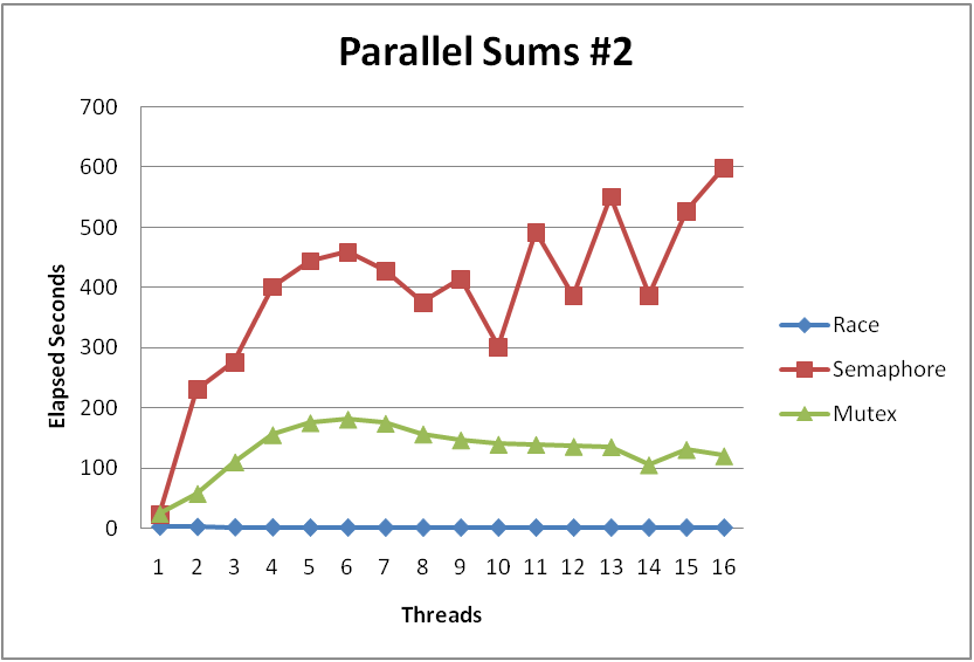
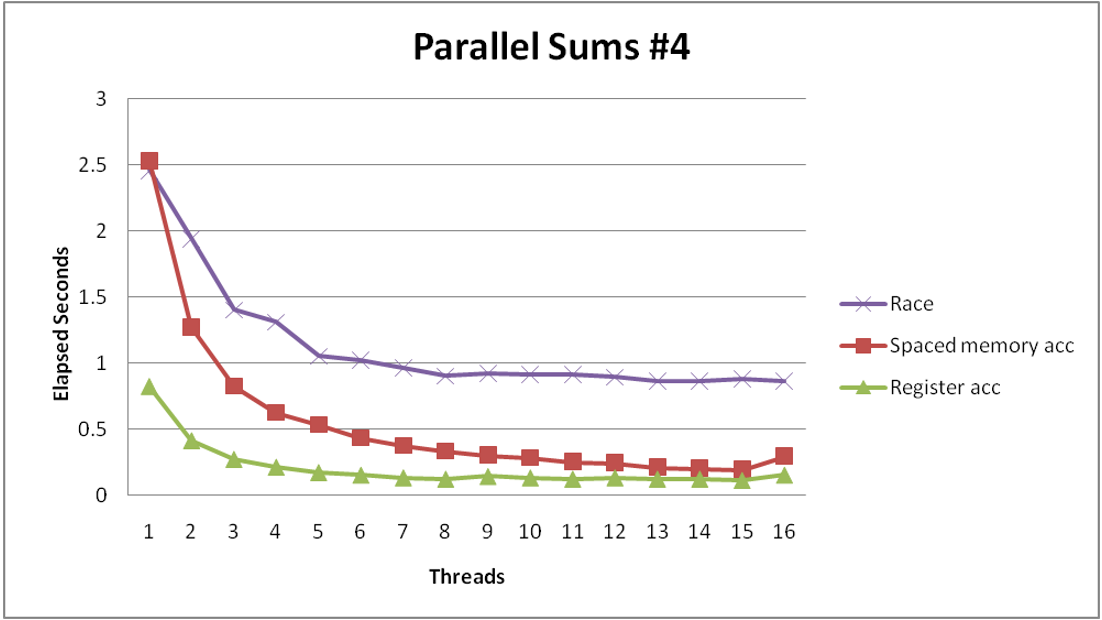
Performance is much worse than the version with the data race! Our threads are spending all their time fighting for the lock, so we essentially have sequential code with the extra overhead of locking and unlocking for every element in the array.
Method #2: each thread accumulates into separate variables
- 2A: Accumulate in contiguous array elements
- 2B: Accumulate in spaced-apart array elements
- 2C: Accumulate in registers
New global variables:
/* Partial sum computed by each thread */ data_t psum[MAXTHREADS*MAXSPACING]; /* Spacing between accumulators */ size_t spacing = 1;
New coordinating code:
nelems_per_thread = nelems / nthreads; /* Create threads and wait for them to finish */ for (i = 0; i < nthreads; i++) { myid[i] = i; psum[i*spacing] = 0; Pthread_create(&tid[i], NULL, thread_fun, &myid[i]); } for (i = 0; i < nthreads; i++) Pthread_join(tid[i], NULL); result = 0; /* Add up the partial sums computed by each thread */ for (i = 0; i < nthreads; i++) result += psum[i*spacing]; /* Add leftover elements */ for (e = nthreads * nelems_per_thread; e < nelems; e++) result += e;
New thread function: (no longer need locking because the threads are writing to different places in memory)
void *sum_global(void *vargp) { int myid = *((int *)vargp); size_t start = myid * nelems_per_thread; size_t end = start + nelems_per_thread; size_t i; size_t index = myid*spacing; psum[index] = 0; for (i = start; i < end; i++) { psum[index] += i; } return NULL; }
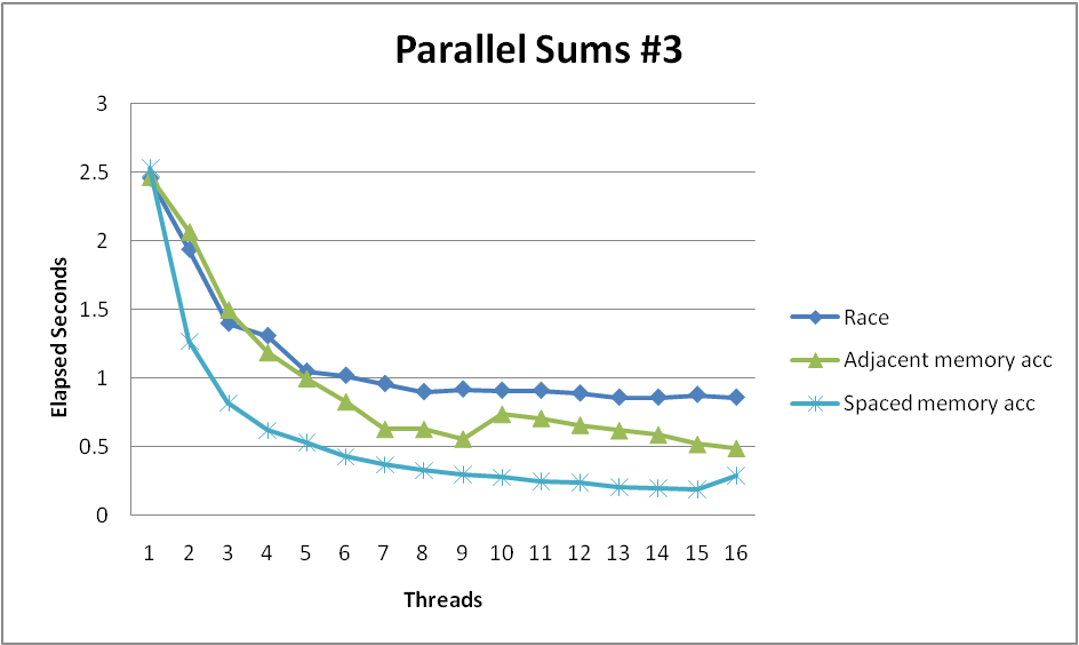
- Clear threading advantage
- Why does spacing the accumulators apart matter?
- The same cache block stored in caches on different cores must be kept consistent (called cache coherence)
- So when thread
iupdatespsum[i], it must have exclusive access to the cache block containingpsum[i], and other cores will have to update their caches - Threads sharing common cache block will keep fighting each other for access to block
- This situation is called false sharing
- Solution: add spacing (padding) between the memory locations threads are updating in order to put them in separate cache blocks
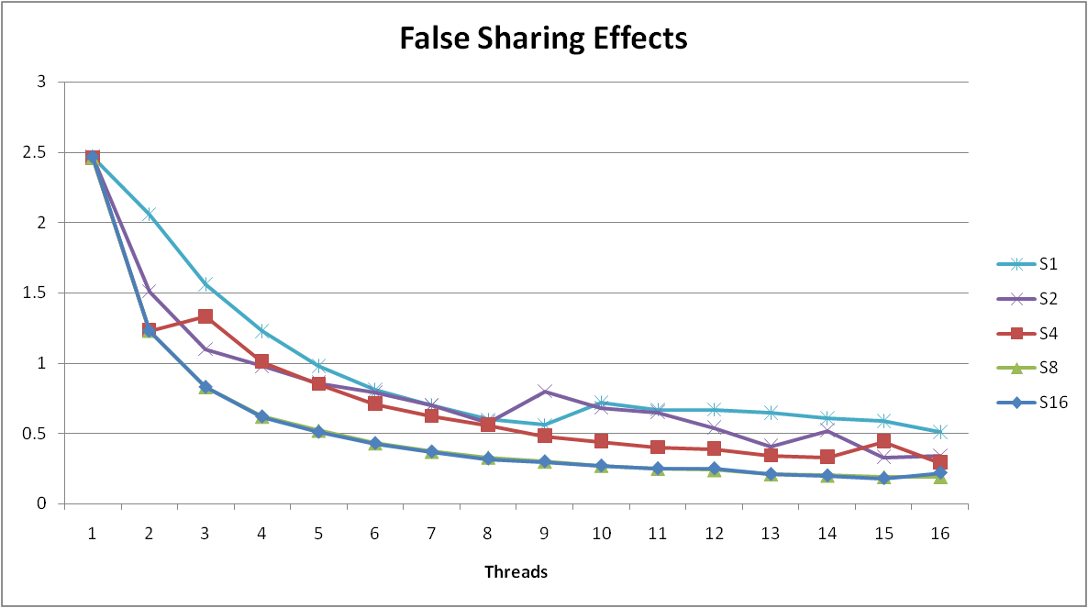
- Demonstrates cache block size = 64
- 8-byte values
- No benefit increasing spacing beyond 8
Better yet, we can do all the additions in a local variable (i.e., a register) and only write to the global array once:
void *sum_local(void *vargp) { int myid = *((int *)vargp); size_t start = myid * nelems_per_thread; size_t end = start + nelems_per_thread; size_t i; size_t index = myid*spacing; data_t sum = 0; for (i = start; i < end; i++) { sum += i; } psum[index] = sum; return NULL; }
3.1 Lessons Learned
- Sharing memory can be expensive
- Pay attention to true sharing
- Pay attention to false sharing
- Use registers whenever possible
- Use local cache whenever possible
- Deal with leftovers
- When examining performance, compare to best possible sequential implementation
4 Limits of Parallelism
- is it faster to pick up a deck of cards with two people instead of 1?
- how about 100 instead of 50?
- there are a finite number of independent tasks, putting a limit on how much can be parallelized
- some tasks need to wait on others, making them inherently sequential
- the amount of speedup that can be achieved through parallelism is limited by the non-parallel portion
5 Amdahl's Law
- Overall problem
- \(T\) Total sequential time required
- \(p\) Fraction of total that can be sped up (\(0 \le p \le 1\))
- \(k\) Speedup factor
- Resulting Performance
- \(T_k = p\frac{T}{k} + (1-p)T\)
- Portion which can be sped up runs \(k\) times faster
- Portion which cannot be sped up stays the same
- Maximum possible speedup
- \(k = \infty\)
- \(T_{\infty} = (1-p)T\)
5.1 Example
- \(T = 10\) Total time required
- \(p = 0.9\) Fraction of total which can be sped up
- \(k = 9\) Speedup factor
- \(T_9 = 0.9 \times \frac{10}{9} + 0.1 \times 10 = 1.0 + 1.0 = 2.0\) (a 5x speedup)
- \(T_{\infty} = 0.1 \times 10.0 = 1.0\) (a 10x speedup)
With infinite parallel computing resources! Limit speedup shows algorithmic limitation
6 Instruction-Level Parallelism
- steps to execute the next x86-64 instruction:
- fetch the instruction
400540: 48 01 fe - decode the instruction
addq %rdi, %rsi - gather data values read
R[%rdi], R[%rsi] - perform operation calc
R[%rdi] + R[%rsi] - store result save into
%rsi
- fetch the instruction
- each of these steps is roughly associated with a part of the processor
- each part can work independently
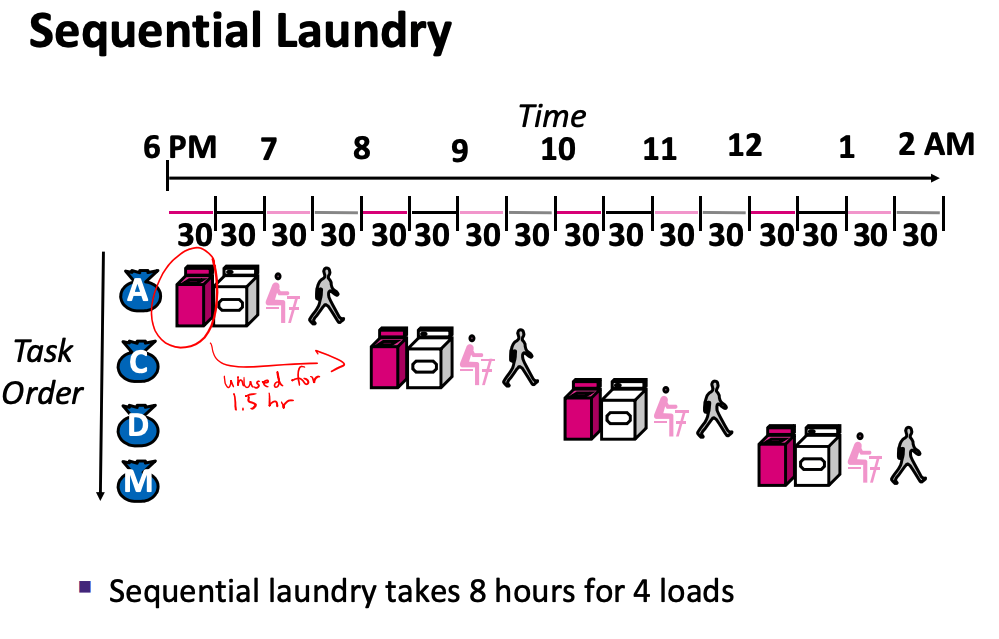
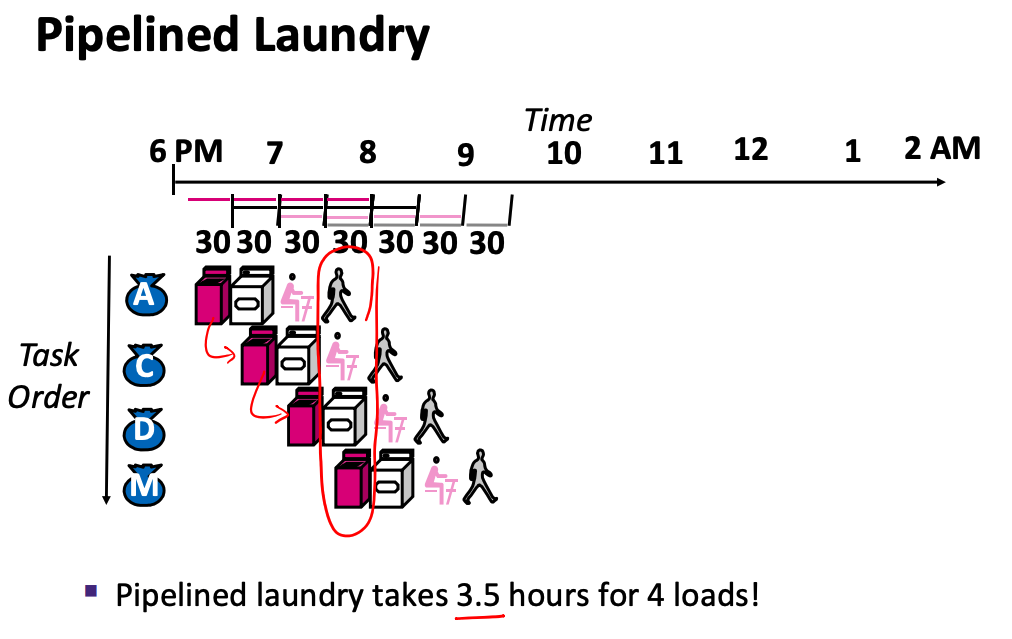
6.1 By Analogy to Doing Laundry
- washer, dryer, folding, and putting away all take 30 minutes
- full task takes 2 hours
- four people doing laundry in sequence takes 8 hours
- but the washer and dryer sit idle for 1.5 hours at a time
- we can start the second load as soon as the first load is done with the washer
- pipelined laundry takes 3.5 hours for 4 loads
- does not improve the latency of a single load (still takes 2 hours), but improves throughput
- processors pipeline instruction execution steps in a similar way