CS 208 s20 — IEEE Floating Point

Table of Contents

1 Introduction

  • We will not cover all the complexities of the 50-page IEEE floating point standard
  • It saved us from the wild west in the early days of computing where every manufacturer was designing their own floating point representation
    • These were typically optimized for performance at the cose of accuracy
  • What do we want from a floating point standard?
    • Scientists/numerical analysts want them to be as real as possible
    • Engineers want them to be easy to implement and fast
    • Scientists mostly won, as floating-point operations can be several times slower than integer operations
  • Basic idea: represent numbers in binary scientific notation

2 Fractional Binary Numbers

The idea of a binary fraction is part of the IEEE representation, so let's start with that.

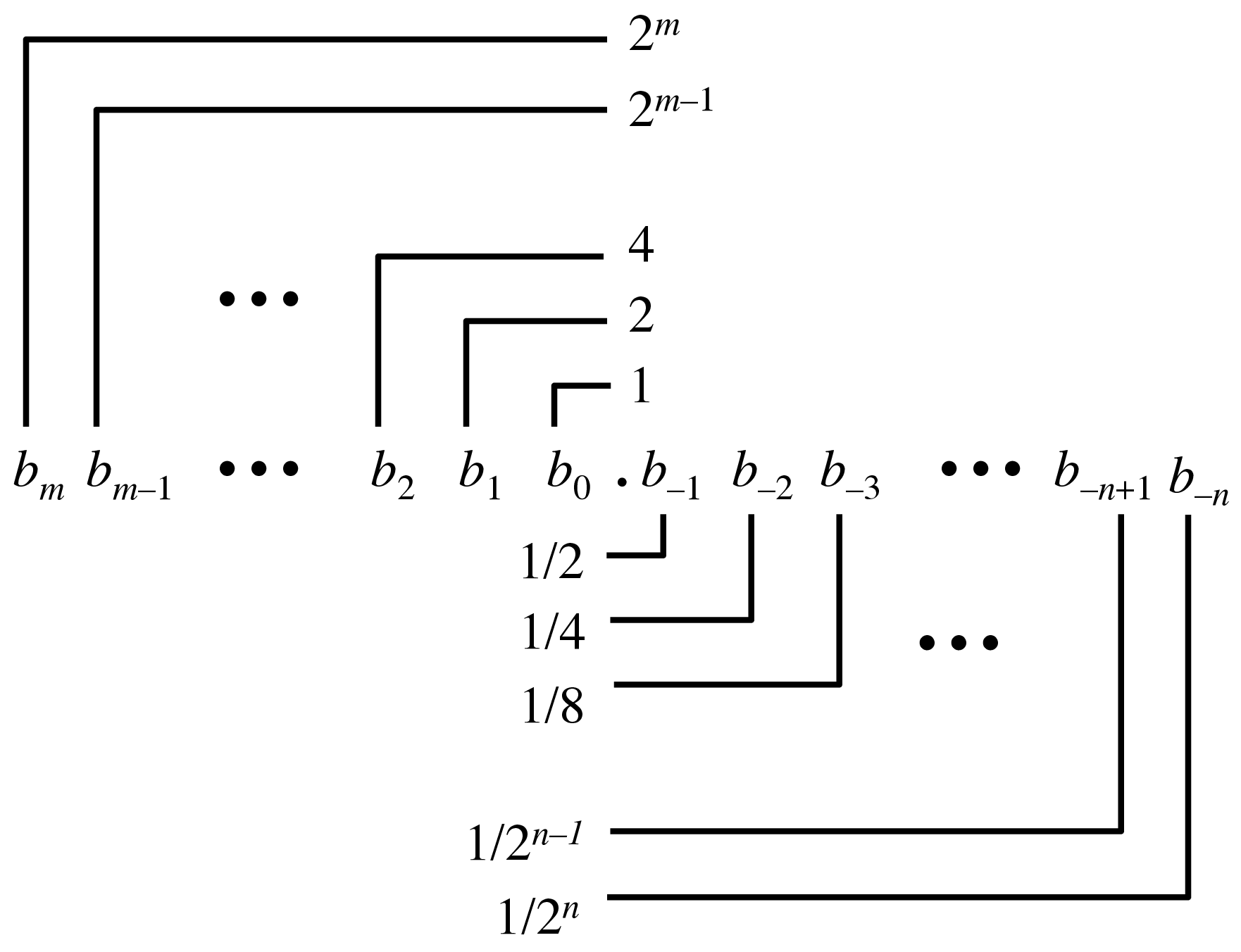
fractional-binary.png

  • Example 0b10.1010 = \(1\times2^1 + 1\times2^{-1} + 1\times2^{-3} = 2.625\)
  • Exercise: what's the closest we can get to 1/3 with 6 bits?1
fraction decimal
1/2 0.5
1/4 0.25
1/8 0.125
1/16 0.0625
1/32 0.03125
1/64 0.015625
  • Exercise: What is the base 10 equivalent of the 6-bit two's complement fixed-point number 0b101.110?2

3 IEEE floating point in 6 bits

  • The value \(V\) of a floating point number is computed using the following formula: \(V = (-1)^s \times M \times 2^E\)
    • sign: \(s\) indicates positive or negative (sign bit when \(V=0\) is special case)
    • significand: \(M\) fractional binary number between 1 and \(2 - \epsilon\) or between 0 and \(1 - \epsilon\)
    • exponent: \(E\) weights by a power of 2 (can be negative power)
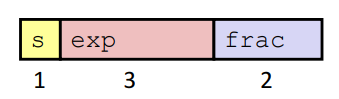
  • We will choose to distribute our 6 bits to represent these quantities as follows:
    • s encodes \(s\)
    • exp encodes \(E\) in biased form
      • normally, \(E\) = exp \(- Bias\) where the \(k\) bits of exp are treated as an unsigned integer and \(Bias = 2^{k-1} - 1\)
    • frac is the binary fraction \(0.f_{n-1}\cdots f_1f_0\), and the significand is \(M = 1 + f\)

ieee-6-bit.png

3.1 Example

  • Take the same six bits from before, 0b1 011 10, what value do they represent under this scheme?
    • s is 1, so value is negative
    • exp is 3, so \(E = 3 - 3 = 0\)
    • frac is 0.5, so \(M = 1 + 0.5 = 1.5\)
    • V = -1.5 × 20 = -1.5

3.2 Exercise

  • With 1 sign bit, 3 exponent bits, and 2 significand bits, how close can we get to 1/33
    • using the formula from the example above

3.3 Why the biased form for exponents?

  • we want to represent very small and very large numbers, so we need the exponent to be signed
    • this suggests encoding exp as a two's complement integer
  • we want floating-point operations to be fast in hardware
    • easier to compare floats if more 1s in exp means bigger number
  • clever trick: store exp as unsigned with implicit bias
    • in fact, by putting exp in between s and frac, the same hardware can do two's complement comparisons and floating-point comparisons

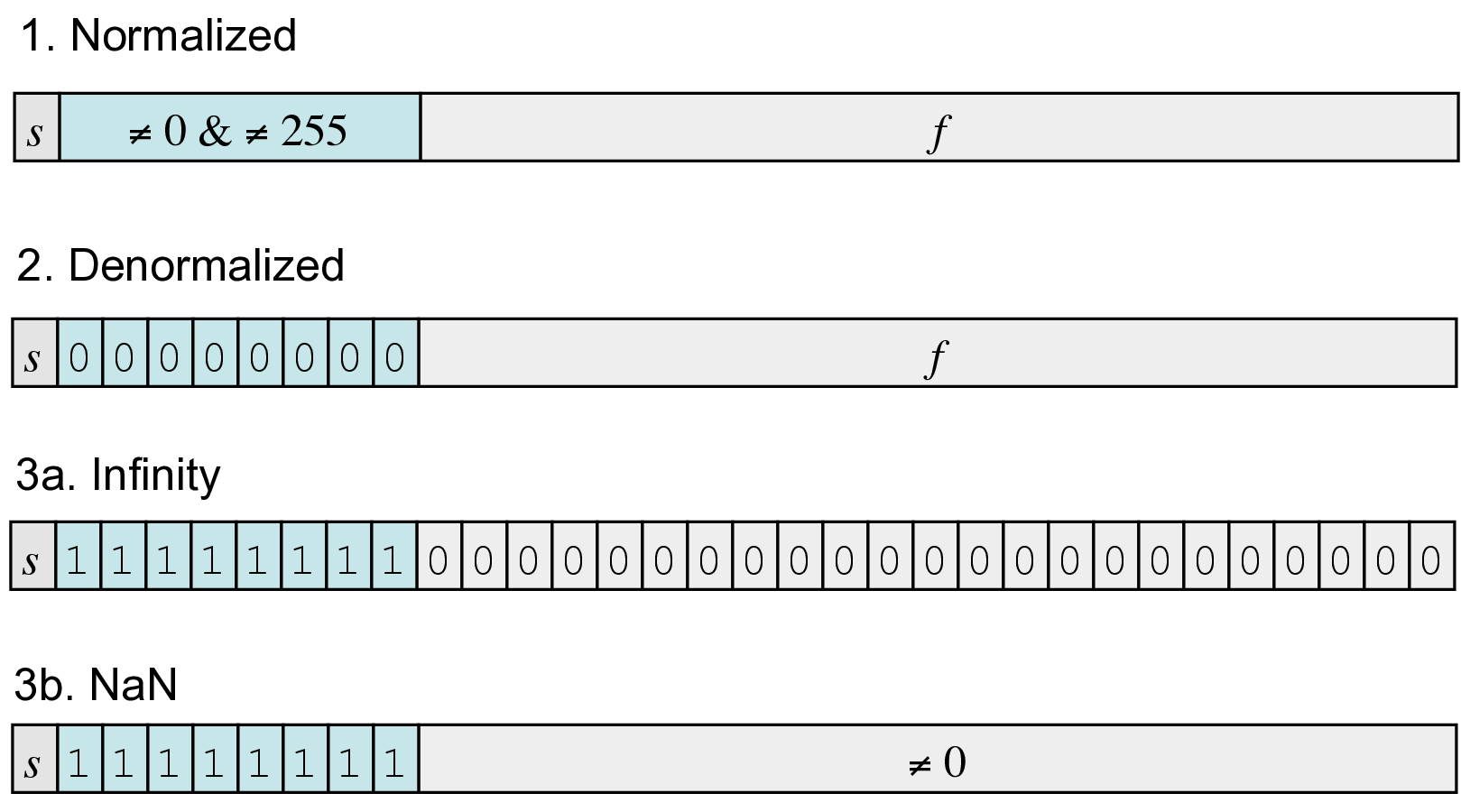
3.4 Denormalized values

  • When exp is 0, the representation switches from normalized to denormalized form
    • \(E = 1 - Bias\)
    • \(M = f\)

4 Real IEEE

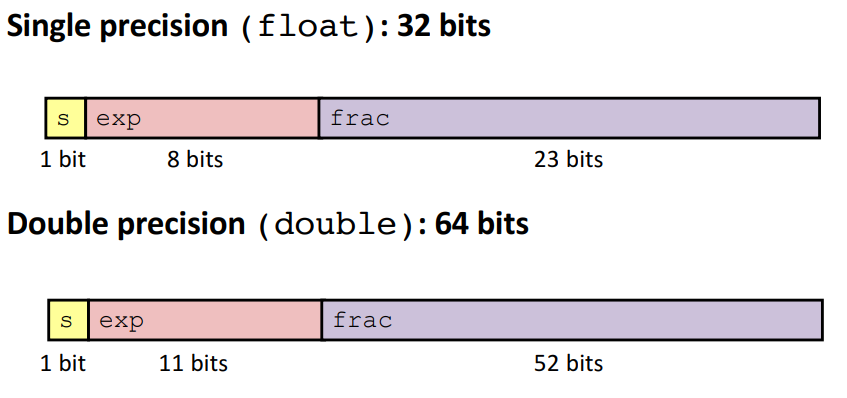
4.1 Reading: IEEE Floating Point Representation

Read section 2.4.2 from the CSPP book (p. 112–115), and take a look at figure 2.34 on p. 115.

ieee-precisions.png

ieee-distribution.png

4.2 Special cases

fp-cases.png

5 Useful simulation

https://www.h-schmidt.net/FloatConverter/IEEE754.html

6 Arithmetic

  • IEEE standard specifies four rounding modes
    • typically round-to-even, helps avoid statistical bias in practice by distributing rounding between rounding up and rounding down
  • In general, perform exact computation and then round to something representable with available bits
    • can underflow if closest representable value is 0
    • can overflow if \(E\) is too big to fit in exp (result is \(\pm\infty\))
    • rounding breaks associtivity

7 Homework

  1. Do practice problem 2.47 in the CSPP book (p. 117)
  2. Remember that lab 0 is due at 9pm tonight (April 20). You can use late days, see the course web page for the late work policy.
  3. Lab 1 has been posted. It will be due 9pm Wednesday, April 29. Part of the provided testing framework, the executable dlc, will only run on a Linux system or VM.

Footnotes:

1

.010101 (1/4 + 1/16 + 1/64 = 0.328125)

2

Two's complement means the most significant bit has negative weight: 0b101.110 = \(-4 + 1 + 0.5 + 0.25 = -2.25\)

3

0 001 01 (sign exponent significand) yields \(1.25 \times 2^{1 - 3} = 1.25 \times 2^{-2} = 0.3125\). This isn't as close as with a 6-bit binary fraction we could structure however we wanted, but an unstructured representation would require extra bits to locate the binary point.