CS 208 s21 — Integer Representation

1. Integer Representation
- 1.1. Why study this low-level implementation detail?
- 1.2. bit weight
2. Unsigned Integers
3. Signed Integer Representation as a Design Problem
- 3.1. 4-bit Sign and Magnitude
- 3.2. 4-bit Two's Complement

1 Integer Representation

Recall the example from the first topic where 200 * 300 * 400 * 500 resulted in -884901888? Over the next two topics studying how integers are represented on computer systems, we will see why exactly this happens.

1.1 Why study this low-level implementation detail?

At first, integer representation may seem like a low-level detail that programmers never have to think about in practice. Why then is it worthwhile to understand deeply? Two main reasons:

Because a vital part of your education at Carleton in general and in courses like 208 specically is looking inside of things and understanding why and how they work. We won't be satisfied with just waving our hands and saying "some arrangement of bits in memory make integers happen, don't worry about it." We'll take this opportunity to deepen our knowledge and see a great example of the concept of an encoding—a set of rules that translate a group of things, in this case integers, into bits.
And because situations where it matters arise in practice and getting it wrong can have very serious consequences
- In 1996 an expensive European Space Agency rocket exploded due to a software crash caused by converting a 64-bit floating point number to a 16-bit signed integer.
- In 2015, it was found that Boeing 787 Dreamliners contained a software flaw, very likely caused by signed integer overflow, that could result in loss of control of the airplane

1.2 bit weight

The way integers are represented involves the concept of a bit's weight. This just means the value that bit contributes to the overall value of a set of bits. For example, the binary number 0b0101 corresponds to 5 in decimal. There are 1s in the 1s place and the 4s place, giving us \(1 + 4 = 5\). We would say the rightmost 1 has a positive weight of 1 and the other 1 has a positive weight of 4.

Stated in a more mathematical way: consider a bit vector \(x\) of width \(w\) with bits \([x_{w-1},x_{w-2},\ldots,x_0]\). When interpreting \(x\) as an integer, we will refer to the value a particular bit contributes as its weight. Usually, the weight of each bit just corresponds to the value it would have in a binary number (i.e., bit \(x_i\) has a weight of \(2^i\))

2 Unsigned Integers

To start with the simpler case, let's look at unsigned integers. Though no type in C uses only 4 bits, I'll be using 4-bit representations to introduce integer concepts. Fewer bits will make it easier to see what's going on and do quick practice problems.

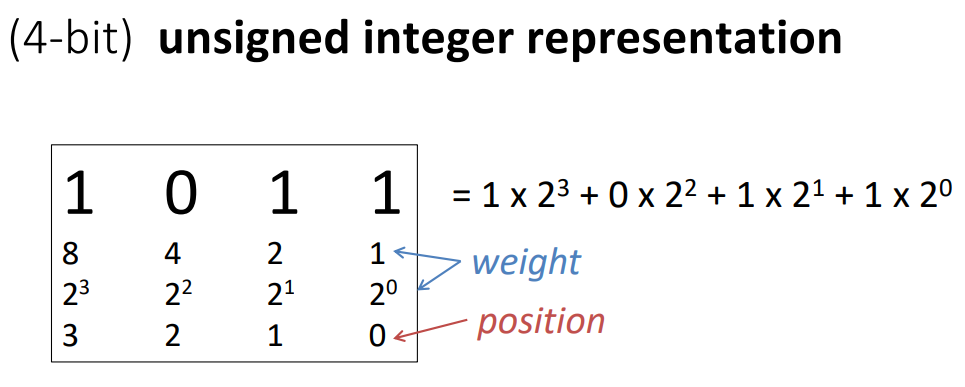
For unsigned integers, we will count each bit as its positive weight. Below are all 16 4-bit unsigned integers in decimal and binary:

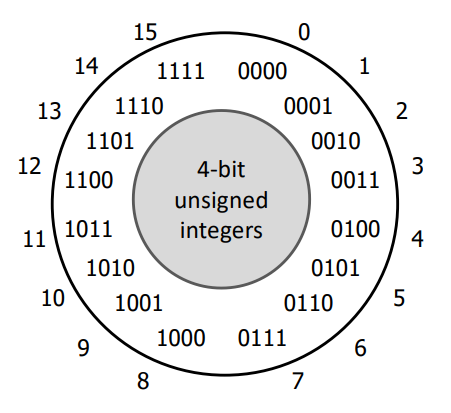
Think about what should happen if we add 1 to 0b1111. Remember we only have 4 bits to work with. You'll see what computers actually do in Wednesday's topic.

3 Signed Integer Representation as a Design Problem

Consider the two following possibilities for a 4-bit signed integer representation:

sign and magnitude: the most significant bit indicates positive (0) or negative (1), the other bits count as their weight
- 0b0011 would be 3, 0b1011 would be -3
two's complement: the most significant bit counts as its negative weight (-8), the other bits count as their positive weight
- 0b0011 would be 3, 0b1101 would be -3 (\(-8 + 4 + 1 = -3\))
- why "two's complement"? Comes from the fact that \(-n\) is represented as the difference of a power of 2 and \(n\), specifically \(2^w - n\)
  - Can see this in 0b1101 for -3: \(w = 4\) (4-bit-wide representation), \(2^4 - 3 = 16 - 3 = 13 =\) 0b1101

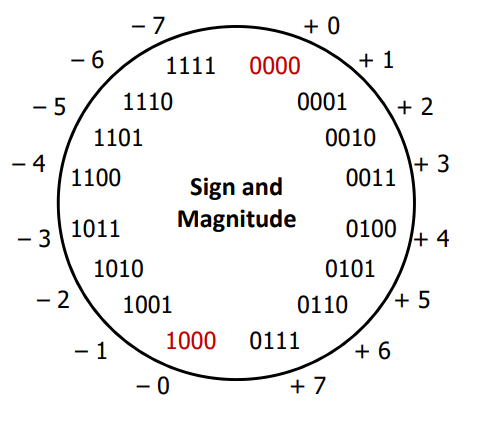
3.1 4-bit Sign and Magnitude

two representations of zero (0b0000 and 0b1000—negative zero??)
arithmetic is cumbersome as negatives "increment" in the wrong direction (i.e., adding 1 to a negative number makes it more negative)

3.2 4-bit Two's Complement

negative numbers "flipped" so that incrementing does what we want
no more -0
preserves nice property of sign and magnitude that positive encodings match unsigned encodings

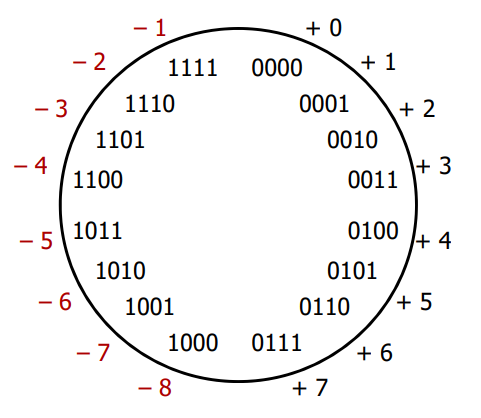
Note that the most significant bit end up still indicating the sign!