CS 208 w20 lecture 3 outline

1 Byte Order

ok, so we know an int at 0x100 consits of the four bytes at 0x100, 0x101, 0x102, and 0x103
- let's say our int has the value 0x2ab600b—which byte goes at which address?
- this depends on the system we're working on (the system's endianness)
if the system stores the least significant byte first, we say it is little endian
- used by x86 (i.e., Intel machines), Andriod, iOS

address	byte
`0x103`	`2a`
`0x102`	`b6`
`0x101`	`60`
`0x100`	`0b`

if the system stores the most significant byte first, we say it is big endian
- used by networks, Oracle, IBM

address	byte
`0x103`	`0b`
`0x102`	`60`
`0x101`	`b6`
`0x100`	`2a`

POLL: We store the value 0x01020304 as a word at address 0x100 in a big-endian, 64-bit machine
- What is the byte of data stored at address 0x104?
- four higher-order bytes are 0x00, stored in 0x100 to 0x103, then 0x01 02 03 04 in 0x104 to 0x107 (making the answer 0x01)
simply a convention or preference, no empirical reason to prefer one over the other
programmer doesn't need to care in most cases
- it matters when data being sent between machines with different endianness
- will need to keep little-endian ordering in mind once we start working with x86-64 assembly

2 Integer Representation

2.1 Why study this low-level implementation detail?

Because situations where it matters arise in practice and getting it wrong can have very serious consequences

In 1996 an expensive European Space Agency rocket exploded due to a software crash caused by converting a 64-bit floating point number to a 16-bit signed integer.
In 2015, it was found that Boeing 787 Dreamliners contained a software flaw, very likely caused by signed integer overflow, that could result in loss of control of the airplane

2.2 bit weight

Consider a bit vector \(x\) of width \(w\) with bits \([x_{w-1},x_{w-2},\ldots,x_0]\). When interpreting \(x\) as an integer, we will refer to the value a particular bit contributes as its weight. Usually, the weight of each bit just corresponds to the value it would have in a binary number (i.e., bit \(x_i\) has a weight of \(2^i\))

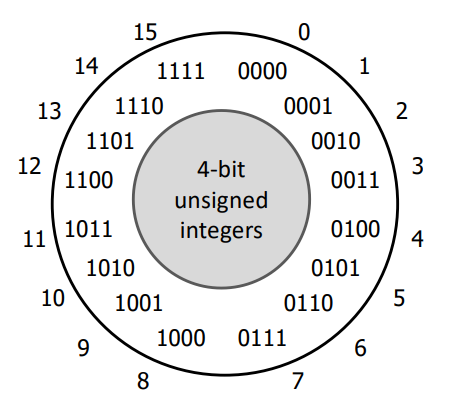
2.3 Unsigned Integers

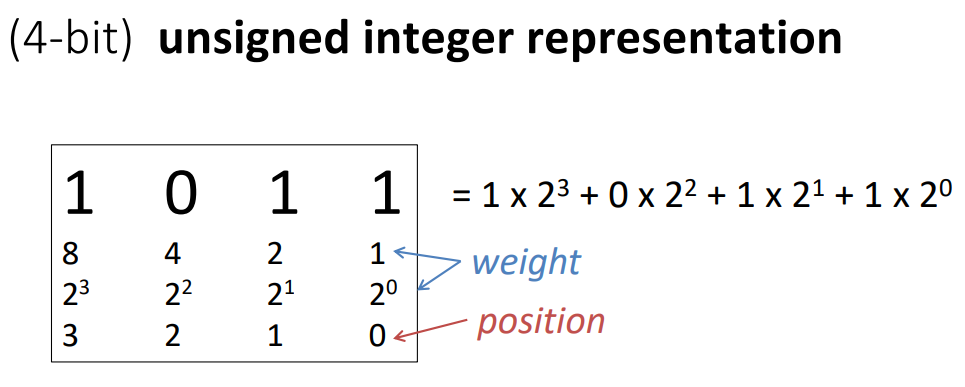Count each bit as its positive weight

2.4 Signed Integer Representation as a Design Problem

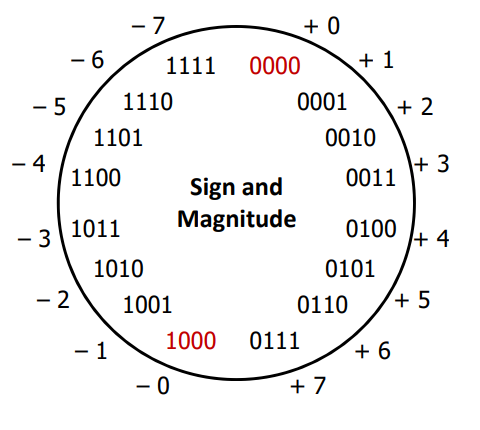
Consider the two following possibilities for a 4-bit signed integer representation:

sign and magnitude: the most significant bit indicates positive (0) or negative (1), the other bits count as their weight
- 0b0011 would be 3, 0b1011 would be -3
two's complement: the most significant bit counts as its negative weight (-8), the other bits count as their positive weight
- 0b0011 would be 3, 0b1101 would be -3 (\(-8 + 4 + 1 = -3\))
- why "two's complement"? Comes from the fact that \(-n\) is represented as the difference of a power of 2 and \(n\), specifically \(2^w - n\)
  - Can see this in 0b1101 for -3: \(w = 4\) (4-bit-wide representation), \(2^4 - 3 = 16 - 3 = 13 =\) 0b1101

What are the benefits and downsides to each of these choices? Think about the set of integer values each can represent, how arithmetic might function, how they might translate to unsigned values.

2.4.1 Sign and Magnitude drawbacks

two representations of zero (0b0000 and 0b1000—negative zero??)
arithmetic is cumbersome as negatives "increment" in the wrong direction (i.e., adding 1 to a negative number makes it more negative)

2.4.2 Two's Complement fixes these

negative numbers "flipped" so that incrementing does what we want
no more -0
preserves nice property of sign and magnitude that positive encodings match unsigned encodings

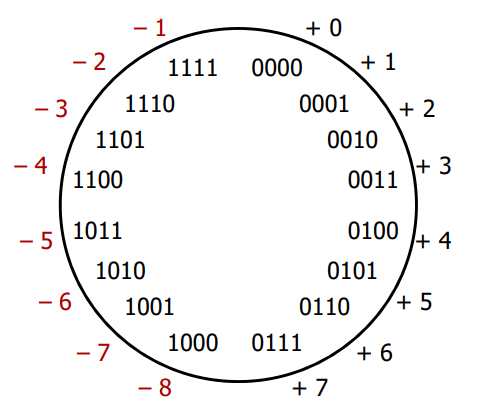Note that the most significant bit end up still indicating the sign!

2.5 POLL

Take the 4‐bit number encoding x = 0b1011
Which of the following numbers is NOT a valid interpretation of x using any of the number representation schemes discussed today? (-4, -5, 11, -3)
- Unsigned, Sign and Magnitude, Two’s Complement