CS 208 s20 — Caching: Basic Principles
Table of Contents
1 Video
Here is a video lecture for the material outlined below. It covers CSPP sections 6.4.1 (p. 615–616). It contains sections on
- flickers (0:04)
- introduction (0:35)
- locality: different types (1:47)
- locality: stride examples (9:05)
- 3D array sum exercise (15:45)
- revisit the memory hierarchy (17:09)
- caching terminology (20:59)
- types of cache misses (25:49)
- real cache hierarchy (Core i7) (30:37)
- cache organization: block offset (34:07)
- cache organization: sets (43:19)
- cache organization: spreadsheet example (49:01)
- cache organization: tags (52:04)
- cache miss example (55:19)
- end notes (59:21)
The Panopto viewer has table of contents entries for these sections. Link to the Panopto viewer: https://carleton.hosted.panopto.com/Panopto/Pages/Viewer.aspx?id=23c6efcd-146a-4f65-8ec3-abc101039f8f
2 Locality
sum = 0; for (i = 0; i < n; i++) { sum += a[i]; } return sum;
- sources of data locality:
- temporal:
sumreferenced in each iteration - spatial: consecutive elements of array
a[]accessed
- temporal:
- sources of instruction locality:
- temporal: cycle through loop repeatedly
- spatial: reference instructions in sequence
2.1 Code With Good Locality Accesses Adjacent Elements
int sum_array_rows(int a[M][N]) { int i, j, sum = 0; for (i = 0; i < M; i++) for (j = 0; j < N; j++) sum += a[i][j]; return sum; }

This is a stride 1 access pattern because we shift by 1 element each access. In general, the lower the stride, the better the locality.
int sum_array_rows(int a[M][N]) { int i, j, sum = 0; for (j = 0; j < N; j++) for (i = 0; i < M; i++) sum += a[i][j]; return sum; }

This is a stride N access pattern because we shift by N elements each access.
Recall the example from topic 1 where switching the order of nested loops caused summing an array to take almost 40 times longer. That was exactly this difference—going from a stride 1 access pattern to a stride N access pattern.
2.1.1 Exercise
What is wrong with this code (and how would you fix it)?1
int sum_array_3D(int a[M][N][L]) { int i, j, k, sum = 0; for (i = 0; i < N; i++) for (j = 0; j < L; j++) for (k = 0; k < M; k++) sum += a[k][i][j]; return sum; }
3 Caching Basics
3.1 Revisiting the memory hierarchy
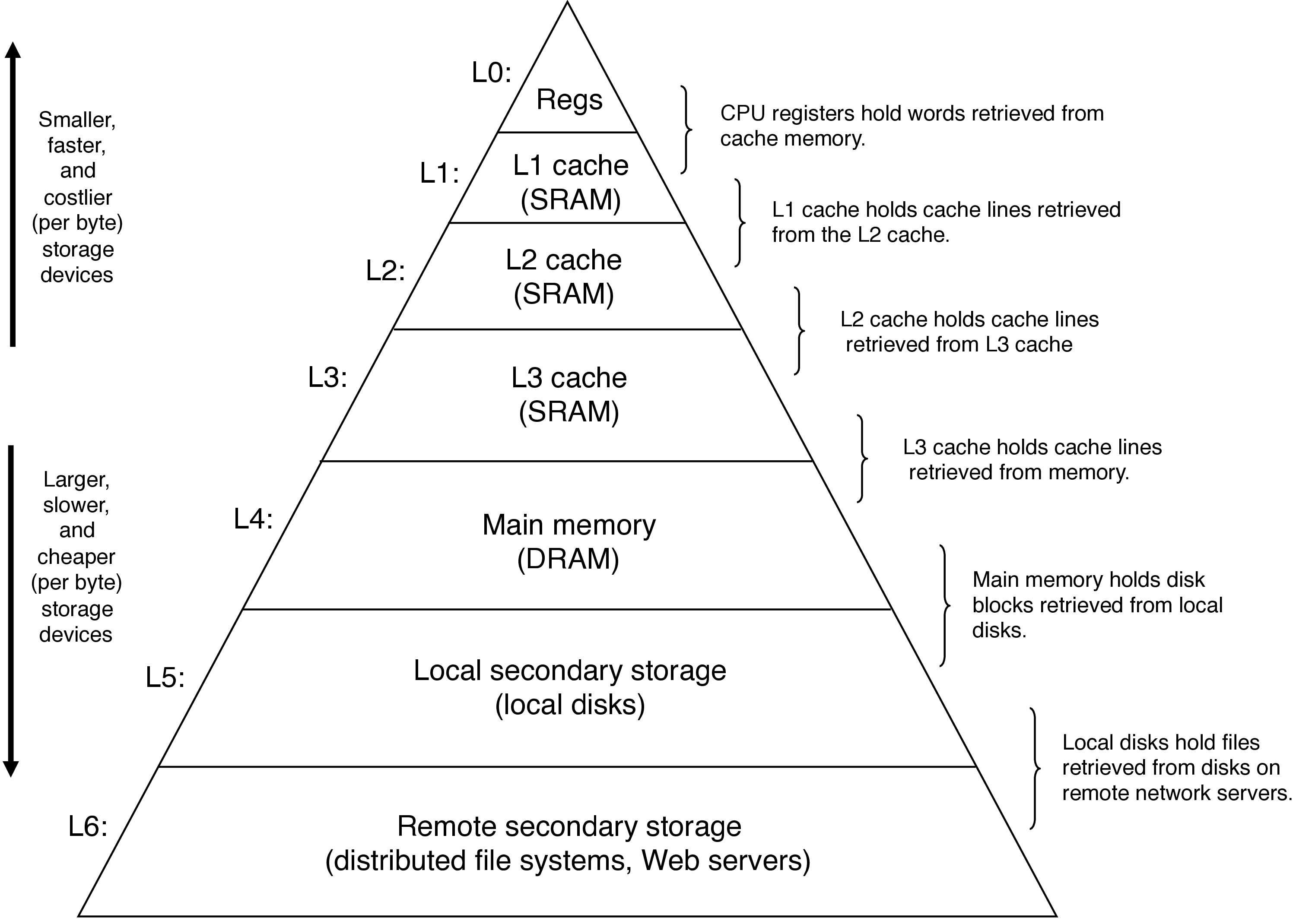
- each level acts as a cache for the level below
- registers explicitly program controlled
- hardware manages caching transparently
3.2 Terminology
3.2.1 cache hits
- finding needed data in level \(k\) instead of \(k + 1\)
3.2.2 cache misses
- having to go to level \(k+1\) because the data is not in level \(k\)
- cache at level \(k\) now contains the data
- if level \(k\) cache is full, it will overwrite an existing block (replacing or evicting)
- which block gets ovewritten governed by the cache's replacement policy
- a random replacement policy would choose randomly
- a least recently used (LRU) policy would choose the block with the oldest last access
3.2.3 kinds of cache misses
- if a cache is empty, every access will result in a cache miss (compulsory or cold misses on a cold cache)
- won't occur once a cache has been warmed up through repeated accesses
- a cache at level \(k\) must have a placement policy to decide where to place a block retrieved from a \(k + 1\) cache
- faster caches tend to implement stricter policy since it's important to be able to locate a block quickly
- e.g., block \(i\) at level \(k+1\) must be placed in block \(i \mod 4\) at level \(k\)
- can lead to a conflict miss (enough room for a block, but placement policy causing a miss, as in cache thrashing between two repeatedly accessed blocks)
- faster caches tend to implement stricter policy since it's important to be able to locate a block quickly
- the set of blocks involved in the current phase of the program (e.g., a loop) is referred to as the working set
- when the working set is too large for a cache, that cache will experience capacity misses
4 Anatomy of a Real Cache Hierarchy
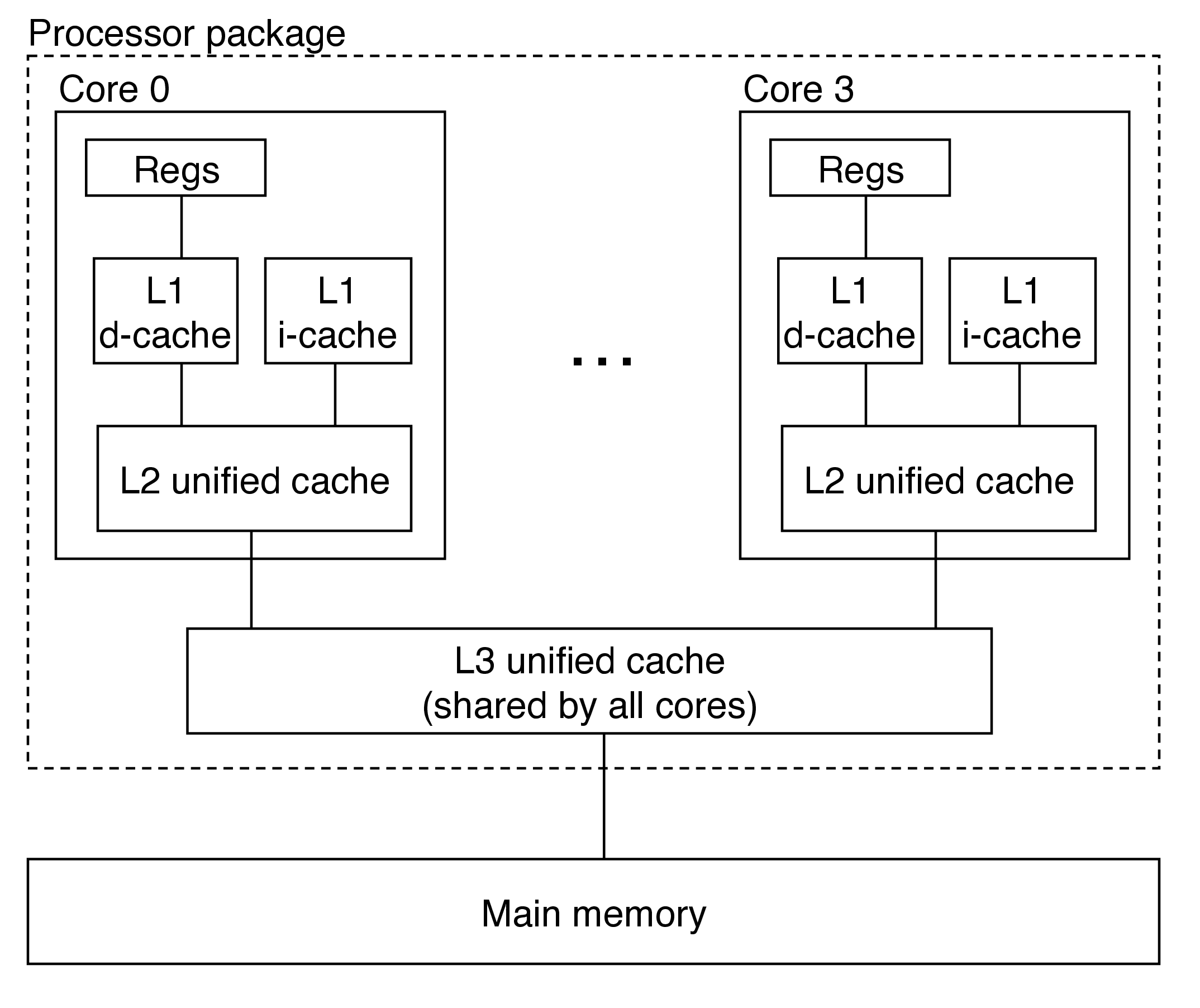
- caches that hold only instructions are i-caches
- caches that hold only data are d-caches
- caches that hold both are unified caches
- modern processors include separate i- and d-caches
- can read an instruction and data at the same time
- caches are optimized to different access patterns
- trades off fewer conflict misses (data and instructions won't conflict) for potentially more capacity misses (smaller caches)
4.1 cache management
- each level must have some managing logic provided by software or hardware
- compiler manages registers
- L1/2/3 managed by hardware logic built into the caches
- usually no action is required on the part of the program to manage caches
5 Cache Organization
5.1 Fundamentals
- the block size \(B\) is the unit of transfer between memory and cache (in bytes, always a power of 2)
- we'll use the low-order \(\log_2 B = b\) bits of a memory address to specify a byte within a block
- the block offset
- for an \(m\)-bit address, the remaining \(m - b\) bits will be used to identify the block (block number)

5.1.1 Quick Check
If we have 6-bit addresses and block size \(B = 4\) bytes, which block and byte does 0x15 refer to?2
5.1.2 Where Should Data Go in the Cache?
- need the procedure for checking if a memory address is in the cache to be fast
- solution: mimic a hash table, a data structure that provides fast lookup
- spreadsheet example
- use middle two bits from address (lower two bits of block number) as set index
- use \(s\) bits to index \(2^s=S\) sets
5.1.3 Example
A request for address 0x2a results in a cache miss. Which index does this block get loaded into and which 3 other addresses are loaded along with it?
- address:
0b 10 10 10, so index10 - block offset is
10, so full block consists of0x28,0x29, and0x2b
5.1.4 What About Collisions?
- access an address not present in the cache, but with the same cache index
- we need to be able to tell this blocks apart
- solution: use leftover address bits as tag bits
- \(t = m - s - b\)
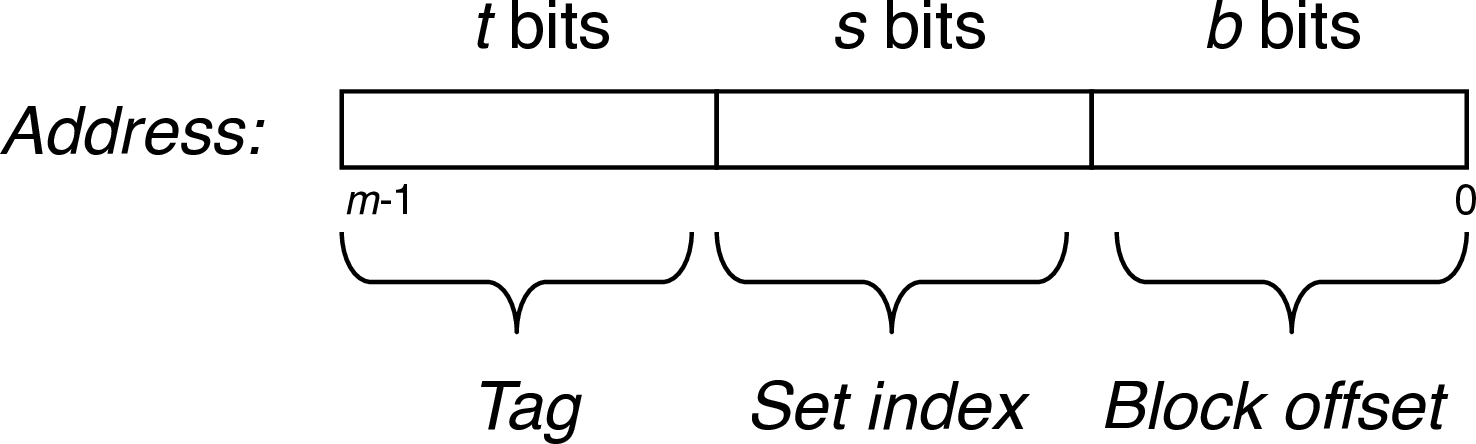
5.1.5 Cache Access
- CPU sends address request for chunk of data
- index field tells you where to look in the cache
- tag field lets you check if the data is block you want
- offset field selects start byte within block
6 Homework
- CSPP practice problems 6.9 (p. 616)
- The week 6 quiz is due 9pm Wednesday, May 20 (tonight)
- Lab 4 will be due 9pm Wednesday, May 27
Footnotes:
The loop ordering results in a very inefficient stride (\(N \times L\)). They can be reordered to achieve a stride 1 access pattern
int sum_array_3D(int a[M][N][L]) { int i, j, k, sum = 0; for (k = 0; k < M; k++) for (i = 0; i < N; i++) for (j = 0; j < L; j++) sum += a[k][i][j]; return sum; }
0x15 is 0b 01 0101 (6-bit address). With a block size of 4, we need 2 bits to specify a byte within a block, leaving the 4 higher order bits as the block number.
Hence, 0x15 refers to byte 0b01 (1) and block 0b0101 (5).