CS 208 s20 — Integer Arithmetic
Table of Contents
1 Homework Solutions
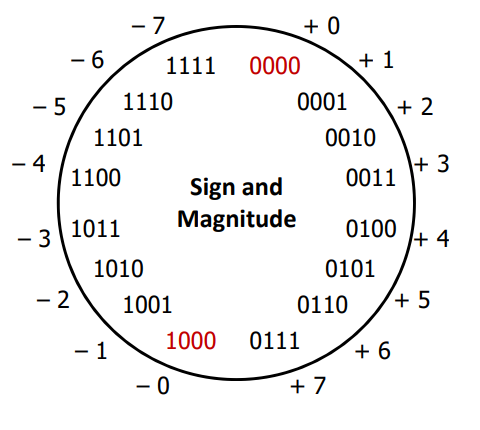
1.1 Sign and Magnitude vs Two's Complement Discussion
- I agree with the point several of you made on the discussion forum that sign and magnitude is more intuitive/easier for humans to deal with by hand. It's probably the first thing I would think of to represent negative binary numbers.
- As many of you pointed out, sign and magnitude two representations of zero (
0b0000and0b1000—negative zero??)- In addition to complications from having two, non-equal versions of 0, this wastes one out of our 16 possible values
- Perhaps more importantly, arithmetic is cumbersome as negatives "increment" in the wrong direction (i.e., adding +1 to a negative number makes it more negative)
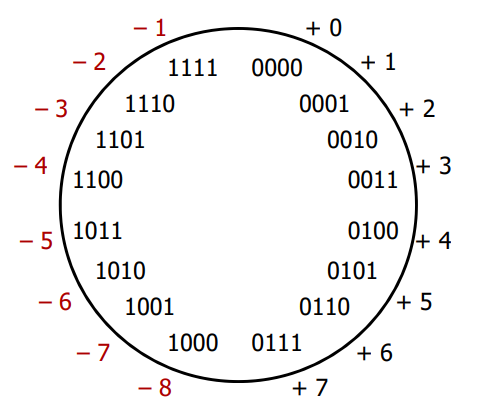
- Two's complement fixes the problems with sign and magnitude
- negative numbers "flipped" so that incrementing does what we want
- no more -0
- It also preserves nice property of sign and magnitude that positive encodings match unsigned encodings
- Note that the most significant bit end up still indicating the sign!
Considering 8-bit integers:
- What is the largest integer?
Unsigned: Two's Complement: 255 127 - How do you represent (if possible) the following numbers: 39, -39, 127?
Unsigned Two's Complement 39:0b0010011139:0b00100111-39: not possible-39:0b11011001127:0b01111111127:0b01111111
2 Warmup
What base-10 integers do these 8-bit quantities represent using two's complement?1
0b000010010b100000010b111111110b00001111
3 Two's Complement Arithmetic
- the same procedure works for both unsigned and two's complement addition
- add the bits as you would expect, discard any that carry out of the most significant bit
- example: \(4 + (-3)\) =
0100 + 1101=10001=0001= \(+1\)
- example: \(4 + (-3)\) =
- add the bits as you would expect, discard any that carry out of the most significant bit
- this is handy because it means the same hardware can perform both signed and unsigned addition
3.1 Practice
Verify that binary addition produces the correct two's complement result for these expressions:2
- \(-2 + -3\)
- \(2 + -3\)
3.2 Additive inverse
Important that for all \(x\), the bit representation of \(x\) and the bit representation of \(-x\) sum to 0 (\(mod\ 2^w\)). That is, it had better be the case that \(x + (-x) = 0\) (throwing away any bits that carry out off the left side) Find the 8-bit negative encodings for these three bit vectors and verify that the sum of the two is 0:3
0b000000010b000000100b11000011
Additive inverses are well behaved for two's complement. We'll see how to quickly find the additive inverse in binary in Friday's topic.
4 Overflow
- Overflow occurs when the result of a computation can't be represented by the current encoding
- For example, \(6 + 3\) =
0110 + 0011 = 1001= \(-7\)- The expected result of \(6+3=9\) exceeds the range of positive numbers 4-bit two's complement can represent
4.1 Fixed-width arithmetic is modular
When we have a fixed number of bits (e.g., 4-bit two's complement), arithmetic becomes modular.

The result of an addition is the sum modulo \(2^w\) (in raw binary—it's then up to the program whether the result is interpreted as signed or unsigned). Intuitively, think of fixed-width arithmetic as wrapping around when it goes too positive or too negative. With 4-bit two's complement, subtract 1 from -8 and it overflows to +7. Similarly, add 1 to +7 and it overflows to -8.
Here we finally see why int x = 200 * 300 * 400 * 500 results in a large negative value.
The result of the multiplication overflows the largest positive value than can be represented by a 32-bit int and wraps around into negative values.
5 Sign Extension
Which of the following 8-bit numbers has the same signed (2's complement) value as the 4-bit number 0b1100?4 (spaces added for readability)
0b 0000 11000b 1000 11000b 1111 11000b 1100 1100
When converting signed integer to a larger integral type, extend with copies of the most significant bit (i.e., sign bit)
- 4-bits to 8-bits:
- 5 goes from
0101to00000101(still 5) - -5 goes from
1011to11111011(still -5)
- 5 goes from
- Called sign extension because we maintain the same value by extending the sign bit to fill in the new bits
- This is what C will do if you cast a smaller signed integer type to a larger one (i.e., cast an
intto along) - Casting unsigned types does not perform sign extension, the new bits are filled with zeros (zero extension).
- This is what C will do if you cast a smaller signed integer type to a larger one (i.e., cast an
6 Truncation
One the other hand, going from a larger integer type to a smaller one just throws away (truncates) the extra bits.
- 8-bits to 4-bits:
- 23 goes from
00010111to0111(now 7) - -23 goes from
11101001to1001(now -7)
- 23 goes from
7 Homework
- Read section 2.2.8 Advice on Signed vs Unsigned in the CSPP book (p. 83–84) and do practice problems 2.25 and 2.26
- These highlight the practical application of understanding integer representations
- CSPP practice problem 2.29 (p. 93)
- They use \(+\) to mean "normal" addition (not modular) and \(+_5^t\) to mean 5-bit two's complement addition
- The case refers to the for possibilities in Figure 2.24
- \(x + y\) is negative and \(x +_5^t y\) overflows to a positive result
- \(x + y\) is negative and \(x +_5^t y\) does not overflow (also negative)
- \(x + y\) is positive and \(x +_5^t y\) does not overflow (also positive)
- \(x + y\) is positive and \(x +_5^t y\) overflows to a negative result
- Start lab 0! For real! No joking around!
- Remember that the Week 1 quiz must be completed by 9pm April 15.
Footnotes:
Convert these bit vectors to decimal integers using two's complement
0b00001001= 90b10000001= -1270b11111111= -10b00001111= 15
Verify binary addition produces the correct result:
- \(-2 + -3 =\)
0b1110 + 0b1101
| 1 | 1 | 1 | 0 | |
|---|---|---|---|---|
| + | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| _ | 1 | 0 | 1 | 1 |
final result: 0b1011 = \(-5\)
- \(2 + -3 =\)
0b0010 + 0b1101
| 0 | 0 | 1 | 0 | |
|---|---|---|---|---|
| + | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
final result: 0b1111 = \(-1\)
Find the additive inverses, verify the sum is 0:
0b00000001= 1, inverse is \(-1\) =0b11111111
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
|---|---|---|---|---|---|---|---|---|
| + | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| _ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0b00000010= 2, inverse is \(-2\) =0b11111110
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|
| + | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| _ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0b11000011= \(-61\), inverse is \(61\) =0b00111101
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
|---|---|---|---|---|---|---|---|---|
| + | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| _ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
What is the 8-bit equivalent of 0b1100 (\(-4\))
0b 0000 1100is 120b 1000 1100is \(-116\)0b 1111 1100is \(-4\) (correct answer)0b 1100 1100is \(-52\)