CS 208 w20 lecture 4 outline

1 Warmup

What two's complement numbers do these 8-bit quantities represent?

0b00001001 (9)
0b10000001 (-127)
0b11111111 (-1)
0b00100111 (39)

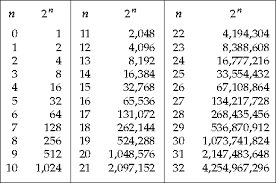
For an $n$-bit representation, what are the minimum and maximum two's complement numbers? Unsigned?

TMax = $2^{n-1} - 1$, TMin = $-2^{n-1}$
UMax = $2^n - 1$, UMin = 0

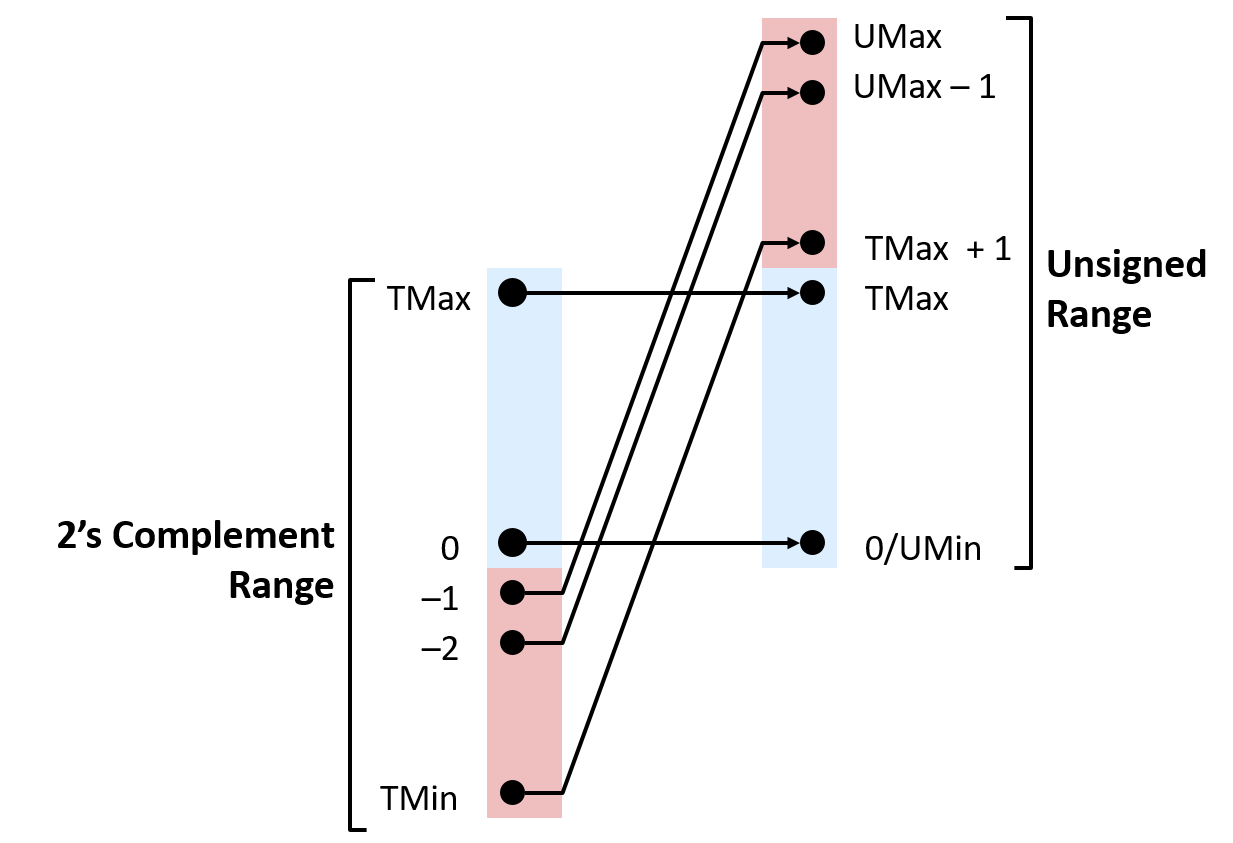
2 Signed vs Unsigned

3 Two's Complement Arithmetic

the same procedure works for both unsigned and two's complement addition
- add the bits as you would expect, discard any that carry out of the most significant bit
  - example: $4 + (-3)$ = 0100 + 1101 = 10001 = 0001 = $+1$
this is handy because it means the same hardware can perform both

3.1 Practice

$-2 + -3$
$2 + -3$

3.2 Additive inverse

Important that for all $x$, the bit representation of $x$ and the bit representation of $-x$ sum to 0 ($mod\ 2^w$). What are the 8-bit negative encodings for

0b00000001
0b00000010
0b11000011

We can derive negation as follows:

x + ~x = 0b11...11
x + ~x = -1
x + ~x + 1 = 0
~x + 1 = -x

4 Overflow

Overflow occurs when the result of a computation can't be represented by the current encoding
$6 + 3$ = 0110 + 0011 = 1001 = $-7$

4.1 Fixed-width arithmetic is modular

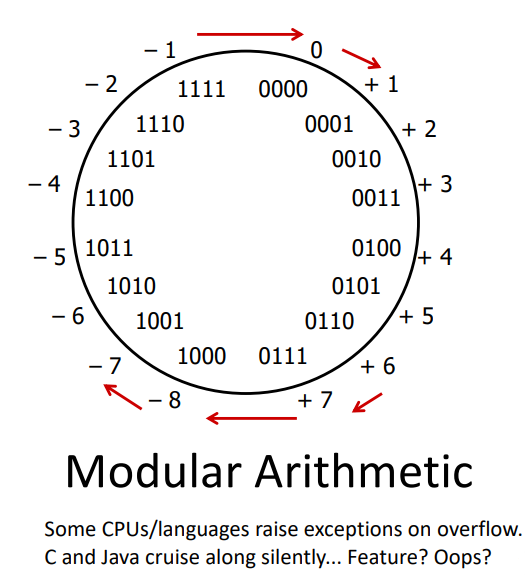
Result of an addition is the sum modulo $2^w$ (in raw binary—it's then up to the program whether the result is interpreted as signed or unsigned).

5 Sign Extension

5.1 POLL

Which of the following 8‐bit numbers has the same signed value as the 4‐bit number 0b1100?

0b 0000 1100
0b 1000 1100
0b 1111 1100 (correct answer)
0b 1100 1100

5.2 When converting signed integer to a larger integral type, extend with copies of the most significant bit (i.e., sign bit)

4-bits to 8-bits:
- 5 goes from 0101 to 00000101
- -5 goes from 1011 to 11111011

5.3 Same idea for arithmetic right shift

compiler uses arithmetic instead of logical when signed values are involved
filling with copies of the most significant bit preserves the sign
- -16>>3 = 11110000>>3 = 11111110 = -2 (consistent with $-16/2^3 = -16/8 = -2$)