Programming Problem Set #2

You must complete four problems in any combination of numbered exercises and challenges. Check-ins will begin around 20:00 the night the problem set is due.

Starter files available here. Download them, right-click on the zip file, and select “Extract All” to unzip. Then open the programming-2-starter folder in VS Code.

python -m pip install numpy matplotlib astropy vpython --no-warn-script-location

Background

for every row in the image:
    for every column in the image:
        set to zero the green value of the pixel in this row and this column  

The files for this lab are contained in programming-2-starter.zip. Download and unzip it to get started. These files are

• fruit.py: you will modify this file to implement your solution to exercise 0 (Fruit Ninja Academy)

• gray.py: you will modify this file to implement your solution to exercise 1 (Grayscale)

• blue_screen.py: you will modify this file to implement your solution to exercise 2 (Blue Screening)

• blur.py: you will modify this file to implement your solution to exercise 3 (Blur)

• beach_portrait.png: a picture of some backpacking goofball, used as the input image for gray.py

• oz_bluescreen.png: a still photo from the set of the 2013 film Oz the Great and Powerful, used as one of the input images for blue_screen.py

• meadow.png: a peaceful meadow scene, used as one of the input images for blue_screen.py

• reference-beach_portrait_gray.png: the expected output image for gray.py, provided for your reference

• reference-oz_meadow.png: the expected output image for blue_screen.py, provided for your reference

• reference-beach_portrait_blur.png: the expected output image for blur.py, provided for your reference

There are additional files related to the optional challenges as well.

0. Fruit Ninja Academy

Congratulations! The time has come for your final exam at the Fruit Ninja Academy. The array of fruits you will use to demonstrate your slicing prowess has already been assembled in the starter code. You will now face a series of slicing challenges. Extend the provided fruit.py to accomplish the following tasks, printing out the result of each task. The expected number of commands (not necessarily including printing) and expected output are given for each task.

1. Extract the bottom right element in one command.

Tomato

2. Extract the inner 2x2 square in one command.

[['Grapefruit' 'Kumquat']       
 ['Orange' 'Tangerine']]

3. Extract the first and third rows in one command.

[['Apple' 'Banana' 'Blueberry' 'Cherry']       
 ['Nectarine' 'Orange' 'Tangerine' 'Pomegranate']]

4. Extract the inner 2x2 square flipped vertically and horizontally in one command.

[['Tangerine' 'Orange']
 ['Kumquat' 'Grapefruit']]

5. Swap the first and last columns in three commands. Hint: make a copy of an array using the copy() method.

[['Cherry' 'Banana' 'Blueberry' 'Apple']
 ['Mango' 'Grapefruit' 'Kumquat' 'Coconut']
 ['Pomegranate' 'Orange' 'Tangerine' 'Nectarine']
 ['Tomato' 'Raspberry' 'Strawberry' 'Lemon']]

6. Replace every element with the string "SLICED!" in one command.

[['SLICED!' 'SLICED!' 'SLICED!' 'SLICED!']
 ['SLICED!' 'SLICED!' 'SLICED!' 'SLICED!']
 ['SLICED!' 'SLICED!' 'SLICED!' 'SLICED!']
 ['SLICED!' 'SLICED!' 'SLICED!' 'SLICED!']]

1. Grayscale

Modify gray.py to convert image to a black-and-white or grayscale version of the original. In the RGB color model, gray tones are produced when the values of red, green, and blue are all equal. A simple way to do this conversion is to set the red, green, and blue values for each pixel to the average of those values in the original image. That is \(R_{gray} = G_{gray} = B_{gray} = \frac{R + G + B}{3}\). When you have implemented a correct solution, running gray.py should produce a file called beach_portrat_gray.png that is the same image as reference-beach_portrait_gray.png:

2. Blue Screening

Movies–particularly (non-animated) action movies that use a lot of special effects–often use a technique called blue screening to generate some scenes. The actors in a scene are filmed as they perform in front of a blue screen and, later, the special-effects crew removes the blue from the scene and replaces it with another background (an ocean, a skyline, the Carleton campus). The same technique is used for television weather reports–the meteorologist is not really gesturing at cold fronts and snow storms, just at a blank screen. (Sometimes green screening is used instead; the choice depends on things like the skin tone of the star.) This problem asks you to do something similar.

We can combine an image of, say, James Franco on the set of Oz the Great and Powerful (oz_bluescreen.png) with an image of scenery (meadow.png) by replacing the bluish pixels in the first picture with pixels from a background picture. To do this, we have to figure out which pixels are bluish (and can be changed) and which ones correspond to the actor and props (and should be left alone). Identifying which pixels are sufficiently blue is tricky. Here’s an approach that works reasonably well here: count any pixel that satisfies the following formula as “blue” for the purposes of blue screening: \(B > R + G\).

Modify blue_screen.py to use this formula to replace the appropriate pixels in image with pixels from background. When you have implemented a correct solution, running blue_screen.py should produce a file called oz_meadow.png that is the same image as reference-oz_meadow.png.

3. Blur

Modify blur.py to implement the function blur(img, radius). Your blur function should create and return a blurry version of the image (img). For each pixel, average all of the pixels within a square radius of that pixel. Here’s an example what that means:

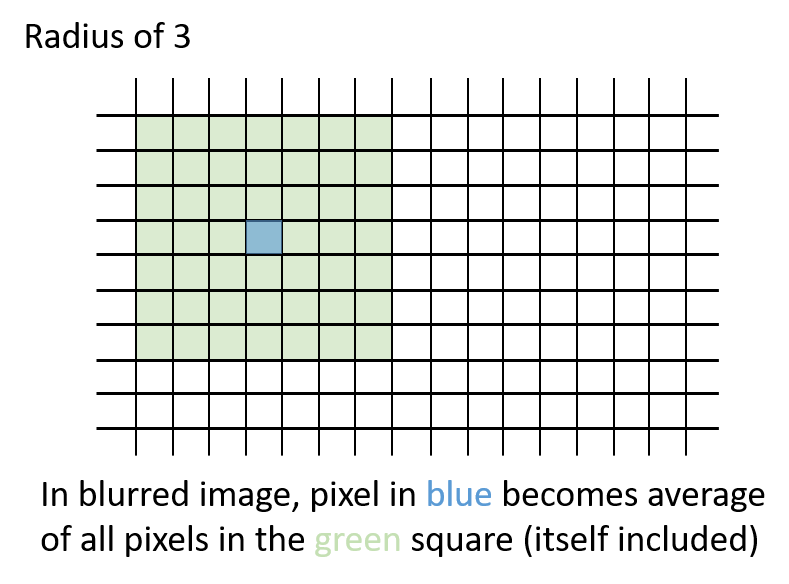
Each pixel will become the average of the square of pixels around it. Pixels at the edges of the image will use whatever part of the square actually exists. Here’s an animation of how the square radius moves with each pixel:

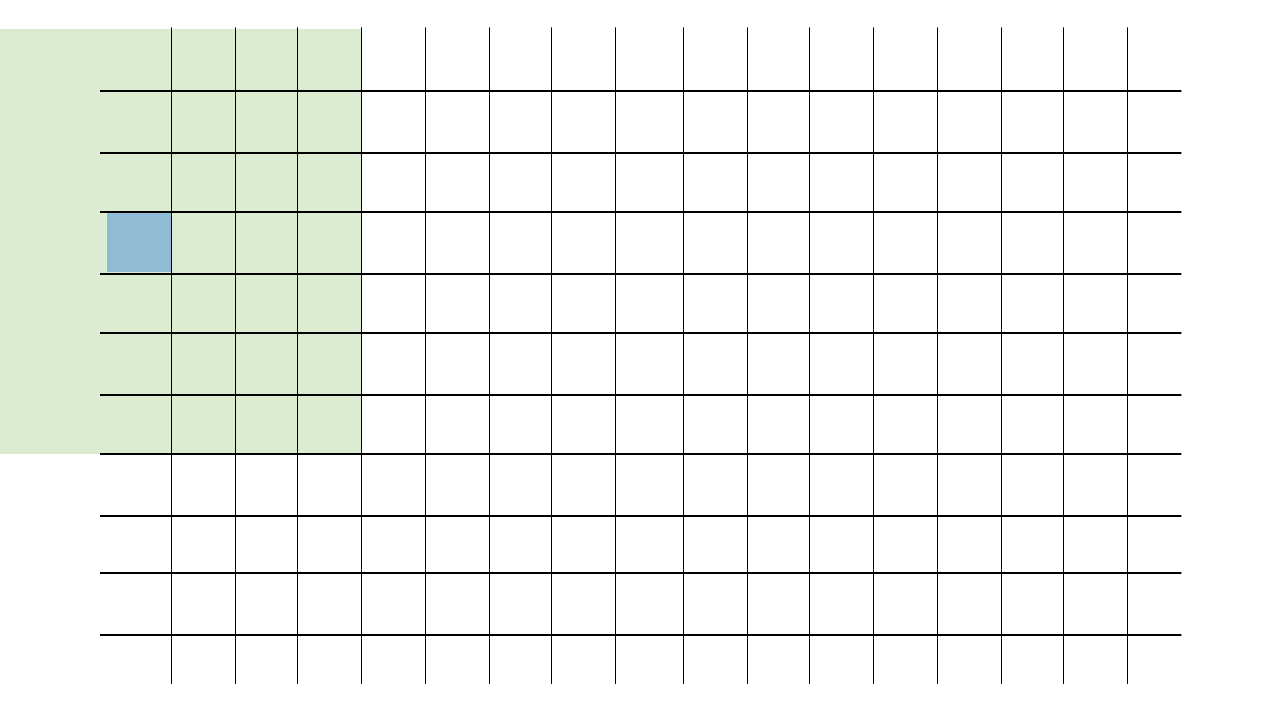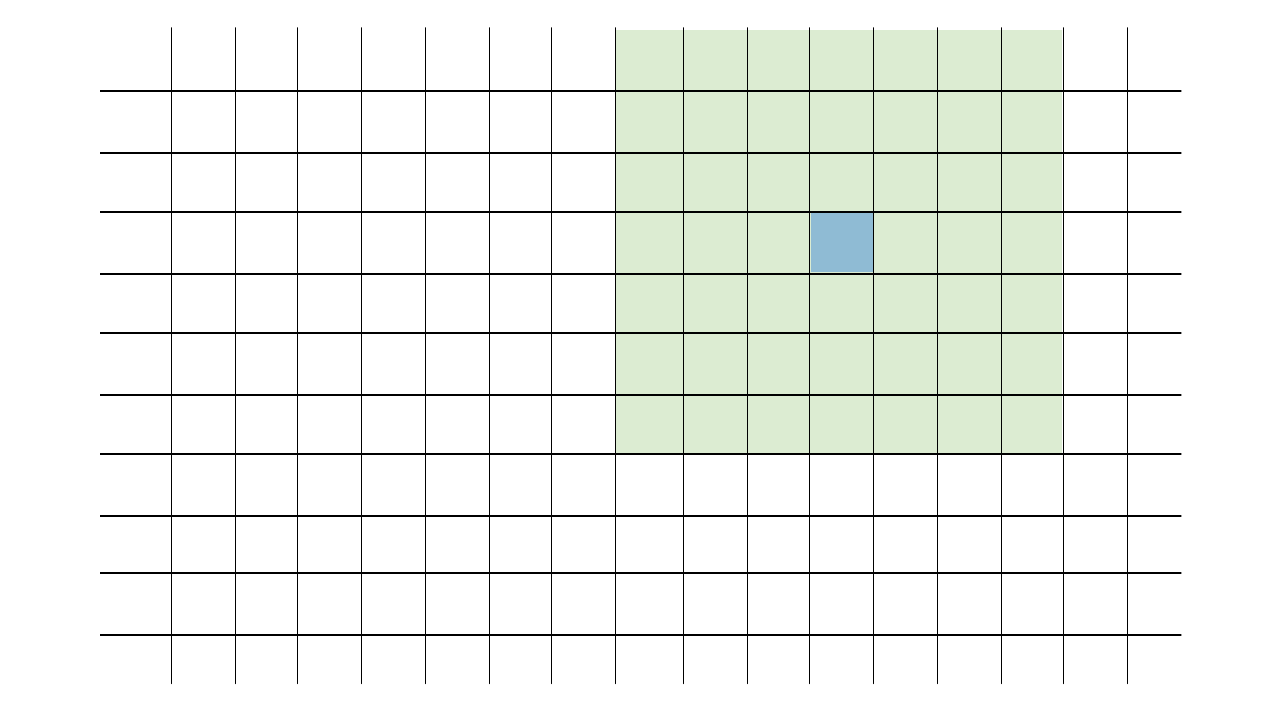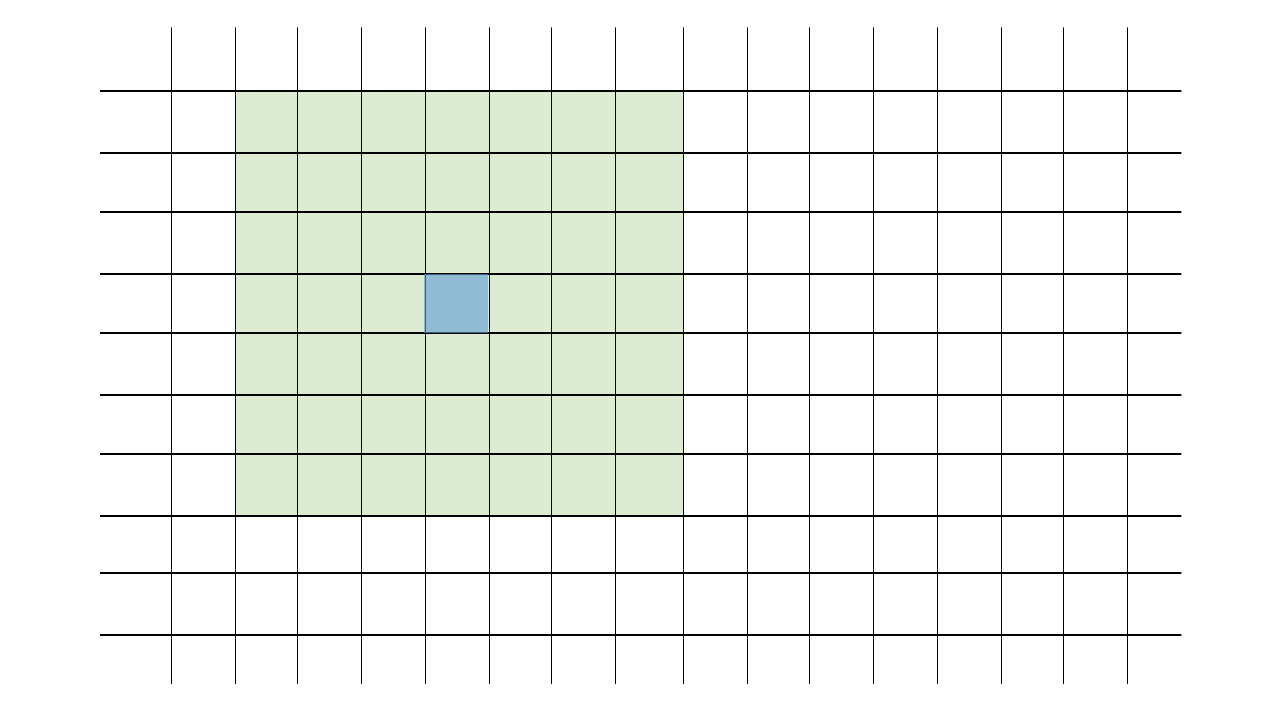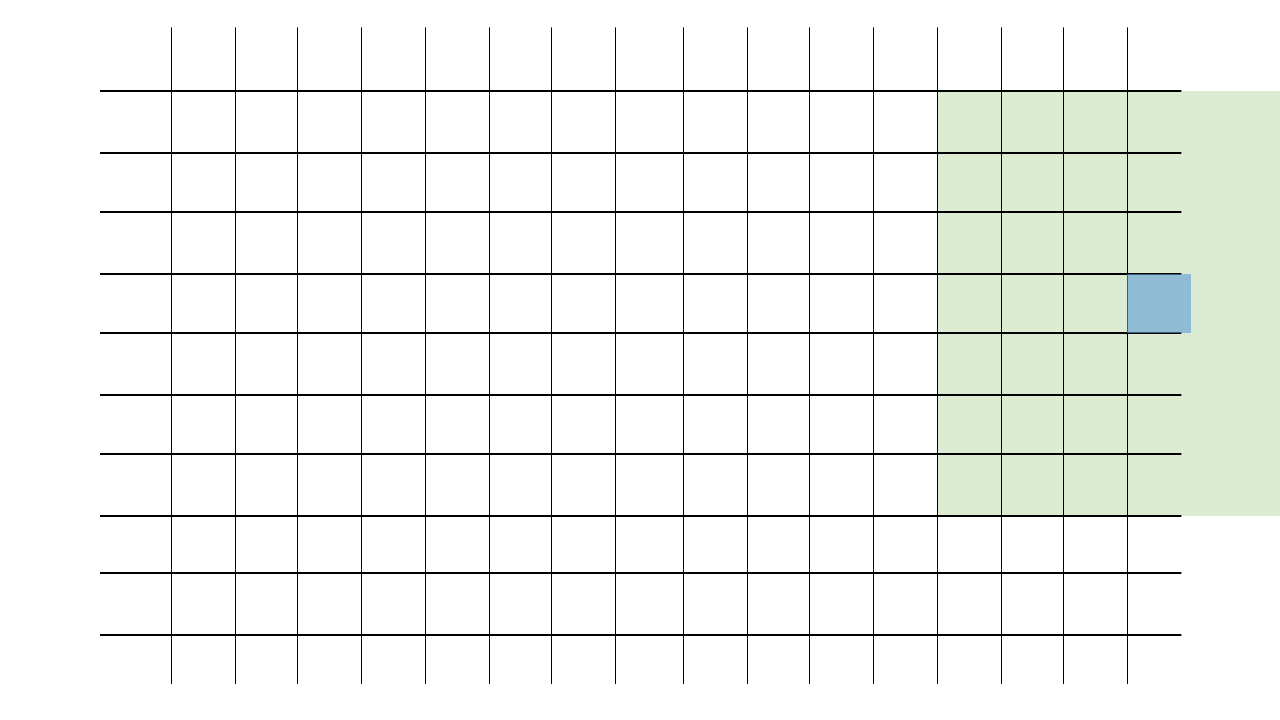
A good way to approach this would be to use radius to slice out a square around the pixel in question. For example, img[0:10, 0:10] would slice out a 10-by-10 square from the upper left corner of the image (note that unlike lists, arrays let us index rows and columns separated by commas instead of multiple sets of brackets). To get the average of the elements of an array you can use .mean() (e.g., img[:, :, 0].mean() would be the average red value for the entire image because it slices out all rows, all columns, and the first element (red) of each pixel).

Make sure to put all of your results in a new image (img.copy() will return a copy of img), instead of overwriting your original as you go; otherwise, your blurred pixels will cascade on top of each other. Be careful near the borders of the image. Keep in mind that some approaches to this problem will result in much slower performance. Any technique that works will receive most of the credit, but your blur.py should run in less than 30 seconds to earn full credit. But do be careful; it’s possible to find solution that take a lot longer!

When you have implemented a correct solution, running blur.py should produce a file called beach_portrait_blur.png that is the same image as reference-beach_portrait_blur.png. Make sure your code calls blur with a radius of 3 like the starter code.

Challenges

C1. Dithering

Dithering is a technique often used to print a gray picture in a legacy medium (such as a newspaper) where no shades of gray are available. Instead, you need to use individual pixels of black and white to simulate shades of gray. A standard approach to dithering is the Floyd–Steinberg algorithm, which works as follows:

1. Loop over all pixels as always, from top to bottom and, within each row, from left to right.
2. For each pixel: if its value is larger than 0.5, then set it to 1.0 (pure white). Otherwise, set it to 0 (pure black). Since this is a grayscale image, the red, green, and blue channels will all be equal. Record the error, which represents how much blackness we have added to this pixel, by taking the old value of this pixel minus the new one. Note that the error can be positive or negative, depending on whether you adjusted the color blackwards or whitewards.
3. Distribute this pixel’s error to adjacent pixels as follows:
   • Add 7/16 of the error to the pixel immediately to the right (“east”).
   • Add 3/16 of the error to the pixel immediately diagonally to the bottom left (“southwest”).
   • Add 5/16 of the error to the pixel immediately below (“south”).
   • Add 1/16 of the error to the pixel immediately diagonally to the bottom right (“southeast”). Be careful near the edges of the image! If some error should be distributed to a pixel that doesn’t exist (e.g., it’s off the edge of the image), you should just ignore that part of the error.

Some tips: (1) while dithering can be used with color images, it’s more complicated, so start by using gray.py to convert an image to gray before you get started. (2) In order for dithering to work, you must make your changes to the same image that you are looping over. Dithering by reading one image and making your changes on a copy will not work correctly, because the error never gets a chance to accumulate. In other words, make sure that you make a grayscale copy of the image first, and then do all dithering work (looping, reading, writing, etc.) on the copy itself.

Now that you have dithering working for grayscale images, extend your dithering function to work for color images as well. It will need to take the desired number of colors per channel (\(n\)) as an argument. For example, if \(n = 2\), then pixels in the dithered image will have one of two possible values for red (0 or 1.0), and similarly for green and blue (for a total of eight possible colors).

To transform a color in the original image to the corresponding dithered color, you’ll need to round the original color to the closest color in the restricted dithered palette. Be sure to apply error separately for each color channel.

An example output image with \(n = 2\):

C2. Edge Detection

The Sobel edge detection algorithm highlights the edges of objects in an image. It works by detecting areas with a high variation in pixel values (gradients).

Algorithm

The algorithm consists of three steps:

1. Calculate horizontal (\(G_x\)) and vertical (\(G_y\)) gradient values for each pixel in the image.
2. Calculate the final gradient magnitude for each pixel using the calculated \(G_x\) and \(G_y\) values.
3. Set each pixel to black or white based on whether the magnitude exceeds a user-provided threshold

To compute \(G_x\) and \(G_y\) values, use the following Sobel operator kernels:

\[ G_x = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix} \]

\[ G_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix} \]

To apply a Sobel operator kernel to a pixel, you must perform a convolution operation. A convolution is the sum of the element-wise multiplication of the kernel with the surrounding pixel values. Then, the final gradient magnitude \(G\) can be calculated as follows:

\[G = \sqrt{G_x^2 + G_y^2}\]

If the input image is in color, you should first convert it to grayscale, as the algorithm works on grayscale images. You might also exploring blurring the input image to reduce the noise in the detected edges.

Make sure to handle border cases, where the Sobel operator kernel may not fit. One solution is to ignore the borders or use edge padding (e.g., mirroring the pixels adjacent to the border).

Expected Output

An example output image with a threshold of 40% of the maximum pixel value and a radius-2 blur applied to the input image:

C3. Mosaic

In this challenge, you will implement an image mosaic operation that selects a random region in the input image and replaces it with the most similar region in the image. The user provides the width and height of the regions to move and the number of moves to perform.

Algorithm

1. Load the input image using plt.imread.
2. Repeat the number of moves specified by the user:
   1. Select a random region in the image with the user-specified width and height. Let’s call it region1.
   2. Divide the image into a grid of width-by-height regions. Let’s call this set of sub-images targets.
   3. Search targets for the region (let’s call it region2) that is the most similar to region1. Use the mean-squared error (MSE) metric for image similarity.
   4. Swap the pixels of region1 with the pixels of region2.
3. Save the modified image using plt.imsave.

Mean-Squared Error (MSE) Metric

The mean-squared error (MSE) between two equally sized image regions \(A\) (width \(w\), height \(h\)) and \(B\) is defined as:

\[ MSE(A, B) = \frac{1}{w \times h} \sum_{x=1}^w \sum_{y=1}^h (A_{xy} - B_{xy})^2 \]

where \(A_{xy}\) and \(B_{xy}\) are the pixel values at position \((x,y)\) in regions \(A\) and \(B\), respectively. The smaller the MSE value, the more similar the image regions are.

Expected Output

An example output image created by 10,000 moves of 10 pixel-by-10 pixel regions: